Math Begins Something & Mathematical Universe Tamed

Mathematical Universe Tamed

by Ken Costello

Allow me to tell a story that could make math more meaningful to you.
	The beginning of our story begins with nothing, absolutely nothing. Well, there was something. Something we know well, but treat it as nothing. (roll cursor over question mark to see it)
	Nothing has another name. It's called zero. Zero is something and nothing at the same time. Zero requires nothing. And since at this beginning there was nothing, zero existed. In other words it existed without needing someone or some thing to make it.
	If zero existed on its own, then a small part of mathematics existed with it. Matter of fact, zero sits right in the middle of mathematics. It's even called the point of origin. So in our story, zero and a small part of mathematics existed when nothing else could.
	Mathematics has positive and negative numbers with the interesting power to cancel each other out. Start with a positive 1 and combine that with a negative 1, you have zero. In our mathematical universe two quantities can pop into existence and just as easy pop out of existence. Amazingly, even in our physical universe virtual particles pop in and out of existence even in a vacuum.
	Here is an example of a positive and negative number canceling. The positive 1 is a circle brighter than the background. The negative 1 is a circle darker than the background. When they combine, their brightness of each cancel out, and they both are gone.
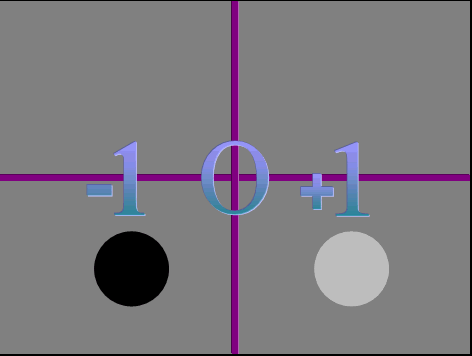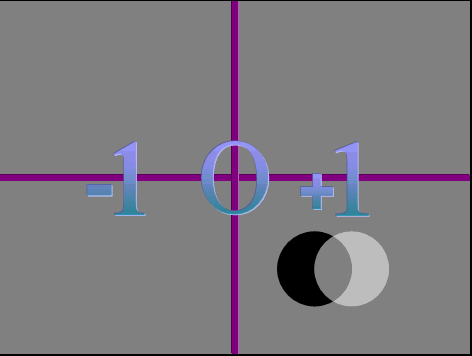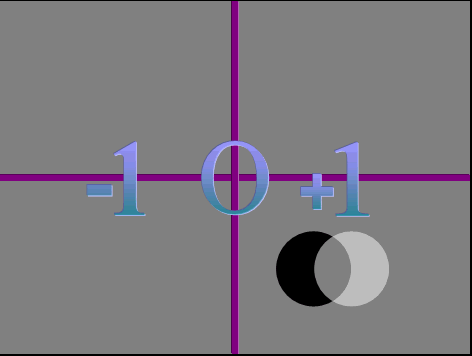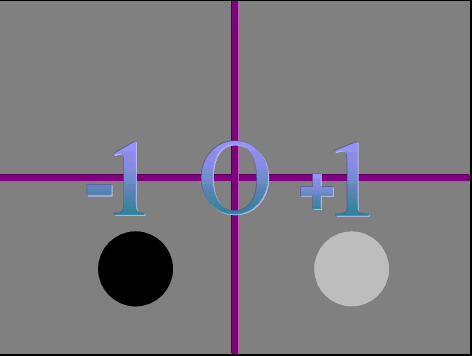
	Even in your world math gives us an illusion of something when there's nothing. For example, people can take out a loan for a million dollars, which gives them a debt of a million dollars. The million dollars will look like they're rich. However, because of the million dollar debt, they actually have nothing. The saying, "A whole lot of nothing" is especially true when zero expands.
	You might think the easiest way to expand our mathematics universe is to count: 1, 2, 3, 4, 5 and so on. If you're Roman, you would count, I, II, III, IV, and V. Counting is a human invention. It helps us communicate a quantity without showing it. Of course 5 is easy, we just hold up all fingers on one hand. Math doesn't need a count. The quantity of 5 is 5 whether or not it is counted.
	Before humans knew how to count, they still were able to keep track of their possessions. For example, if a sheepherder had 10 sheep, he would pick up one stone for the first sheep, a second stone for the second sheep, a third stone for the third sheep and so on. He'd place the stones in a pouch. At the end of the day if he wanted to see if any sheep was missing, he didn't count them, he opened the pouch and took out one stone for each sheep he saw. If there were any stones left in the pouch, he knew that not all sheep were present, and would go out to look for them. Another word for stone is calculus. So our advanced math called "calculus" gets its name from the most simplest of math. Math done with rocks.
	Let's get back to our mathematical universe. It expands with a simple repetition. Of course, the negative counterpart is also being created to keep it balanced to zero. We like to show quantities in a number line because it looks more organized. However, quantities don't have to stay aligned in a row.
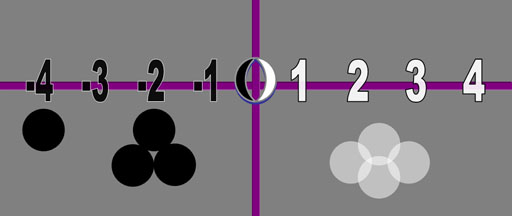
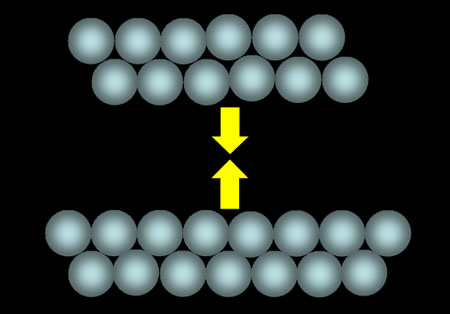
	Since quantities are not restricted to stay in a row, they are free to combine. The first operation of mathematics is born. Addition. Addition is very simple. To add, only means to combine. There's no calculation necessary.
	If asked what is 12 + 15, we typically do the steps of addition and come up with the answer of 27. Realize that addition occurs the moment they are combined. There's really no need to do the steps of addition. Below is a practical example of this.
	If you were building a shelf that needed to be 4 inches high to accommodate a VCR and another 10 centimeters high to stack on a DVD player, how might you add these quantities in order to build the shelf to the right height? You may be inclined to convert centimeters to inches and then add them. Smart carpenters will add them without calculations. First they would measure 4 inches and then extend that length by 10 centimeters, thereby adding the lengths by simply combining them. It's fast and simple.
	The mathematical universe is simple and fast. So fast that it quickly looks complex. For example, take the repetition of adding 1. If real fast, you're at a million, billion, trillion, and up into sizes that will make your head spin. You will top out at infinity, which is so large that there's no going back. In other words, divide your distance by any amount short of infinity and you are still at infinity.
	The Mathematical Universe is much like Music Theory. It has patterns, scales, and all kinds of rules that form the basis of music, but it isn't music. For example, the tempo of a song is measured in beats per minute. Many songs are around 100 beats per minute, but, in theory, you can set a song to any beats per minute you want. How about 10,000 beats per minute? In theory, this is fine, but in practice there are no musicians or instruments that can play that fast, plus it wouldn't sound like music that fast. We need some limits to the Mathematical Universe in order to have music. This is where the Physical Universe comes to the stage.
	If Mathematics is like Music Theory, then the Physical Universe is like a musical performance. The Physical Universe draws from math, but its notes are written for real musicians, real instruments, and are pleasing and recognizable. To do that there has to be some constraints on the music. One such constraint is the speed that it travels. For example, if actual sound waves traveled infinitely fast, there would never be an echo or reverb (a short echo) because the reflections of sound would arrive at the ear at the same time as the direct sound. Reverb adds richness to the sound as you know from hearing a voice or instrument in a large auditorium. In the Physical Universe, light is our "sound" and it can only travel at the speed of light. In music theory (and in math), every time you double the frequency of a vibration, you go an octave higher. In the Physical Universe, however, there's a limit to how high a frequency can go. There's also a limit to to how short time intervals can be and short distance can be.
	Chemistry is here to help explain the Physical Universe. Chemistry, like the Physical Universe, is married to mathematics, but it has a personality that is practical and down to earth. That doesn't mean chemistry is not exotic. There's plenty of that, too, but there are some rules. Where Math can describe things that don't exist, Chemistry helps us deal with things that do exist. In other words, Chemistry is a practical science. However, we can learn from math. Remember I mentioned math has numbers that are opposite (positive and negative). The Physical Universe deals with opposites also. Electrical Charge: Negative and Positive Magnetism: North and South Poles Like in Math, these opposites can cancel each other so that their influence is zero.
	Here's an example of using opposites to cancel. How might you survive an lightning strike? Electrocute yourself. Lightning strikes because a highly negative cloud pushes away electrons on the ground below leaving you and the ground around you positively charged. Electrons are attracted to positive charge and so they come out of the sky to hit you and the ground (lightning strike). However, if you could grab a high voltage negative wire at the right moment (electrocute yourself), the electrons in the high voltage wire will neutralize your positive charge, thus removing you as a target of the lightning. Of course the timing would have to be perfect, but in theory it would work.
	Math started from nothing, with that nothing being zero. Even with those humble beginnings, it seems math laid down the framework for the Physical Universe. The real musical experience began with the taming of math and by agreeing to some rules we could all play by. So as you study chemistry, learn your math theory, but turn it into a musical experience that can be heard, seen, and enjoyed.

<-CHM-130 Home Page