
You may remember from the metrics tutorial that distance, mass, and volume was based on water. The same is true with some units of energy. This liter bottle will help illustrate these units. If you took the bottle and threw it so that it took one second to make the throw and the bottle was traveling 1 meter per second speed as you let it go, one "joule" of energy was transferred to the bottle. (Joule is named after James Joule) The force that you exerted on the the kilogram of water to get that liter of water up to 1 meter per second is defined as one "newton" of force (Symbol is N). Energy is often calculated as force times distance. So in this case, one newton of force times one meter is called either newton·meter or one joule.



Another unit of energy based on water is the calorie. A calorie is defined as the amount of energy needed to raise 1 gram of water 1 degree Celsius. If it is a kilogram of water (1 liter), they call that a kilocalorie or a food calorie.
In this example. we have a kilogram of water. That would take 1,000 calories to raise it 1 degree Celsius. If going from room temperature (20°C) up to near boiling (90°C), that's a 70 degree increase and therefore 70 x 1000 calories, or 70,000 calories to heat it.



A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | ||||||||||
| 2 | 1 |
kilowatt·hour | 1 |
joule/sec | 1000 | 3600 |
sec | = |
3600000 |
joules |
| 3 | 1 |
watt | kilo | 1 |
hour |


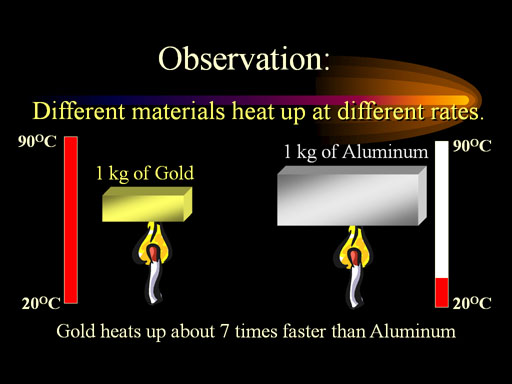
For example, the specific heat of gold is over 30 times smaller than that of water. In other words, a kilogram of gold will go from 20°C to 90°C, while water will only go from 20°C to 22°C when they both are heated equally. The specific heat of gold is 0.031 calories per gram per degree Celsius (0.031cal/g·°C).
Why such a big difference? (See next paragraph(



A more common approach to find the specific heat of a substance (like metals) is to heat that substance and then put it into a known amount of water.
The blacksmith may have been one of the first people to recognize this. They often drop various metals into a bucket of water to cool the metal. They undoubtedly noticed that the water would heat up. They knew the heavier the piece of metal, the more the water would heat up. They may have noticed that different metals of equal weight would not heat up the water to the same temperature.

As we would suspect a hot iron horseshoe dropped into this water will heat up the water at the same time as cooling off the horseshoe. Also, in a minute or so, the horseshoe and water will be the same temperature.
By knowing the mass of the horseshoe, the mass of the water, plus the beginning temperatures of the water and horseshoe, along with the final temperature of the water, we can figure out the specific heat of iron.

The trick to figuring this out is to recognize that the energy lost by the horseshoe will be the energy gained by the water. In other words the calories lost is equal to the calories gained.
Specific heat is calories per gram per degree Celsius. That means if we multiply by grams and degrees Celsius, those units cancel and we are left with just calories (energy)

Let's say this horseshoe weighed 449 grams and was 455°C before dropping into the water. There were 2.00 liters (2,000g) of water, which started out at 24°C and ended up at 34.2°C. What is the specific heat of iron?
Again, we set up an equation that shows the energy lost by the iron equals the energy gained by the water.
Notice in the spreadsheet below that the one °C in the denominator cancel both of the °C in the numerator because after those in the numerator are subtracted, there's only one °C left.
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
T |
U |
|
Energy lost from the horseshoe |
equals |
Energy gained by the water | ||||||||||||||||||
| 1 | unknown specific heat |
mass iron |
Final Temp |
Initial Temp |
specific heat water |
mass water | Final Temp |
Initial Temp |
||||||||||||
| 2 | - |
??? |
calories | 449 |
g | 34.2 |
°C | - |
455 |
°C | = |
1.00 |
calories | 2000 |
g | 34.2 |
°C | - |
24.0 |
°C |
| 3 | g·°C | g·°C | ||||||||||||||||||
| 4 | Formula in I5 is "=D2*(F2-I2)" |
Formula in L5 is "=N2*(P2-T2)" | ||||||||||||||||||
| 5 | - |
??? |
calories | x |
-188939 |
g·°C | = |
20400 |
calories | |||||||||||
| 6 | g·°C | |||||||||||||||||||
| 7 | Solving for unknown specific heat by dividing both sides by 188939 g·°C |
|||||||||||||||||||
| 8 | Formula in I8 is "=L8/L9" |
0.108 |
calories | = |
20400 |
calories | Formula in L8 is "=L5" | |||||||||||||
| 9 | g·°C | 188939 |
g·°C | Formula in L9 is "=I5" | ||||||||||||||||
Here we get the specific heat of the iron in the horseshoe as 0.108 calories per g per °C. If this is entered in a spreadsheet, you can change any of the values in row 2 and the specific heat will automatically be calculated n I8.

A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
T |
|
| 1 | specific heat of water |
volume of pool in cm3 |
cm3 > grams |
temp rise | convert calories to kilowatt-hr |
cost per kilowatt-hr |
$ to heat pool |
||||||||||||
| 2 | 1.00 |
calories | 700 |
cm | 500 |
cm | 200 |
cm | 1 |
gram | 17 |
°C | =1.1*10^-6 |
kilowatt-hr | $ |
0.10 | = |
$ |
??? |
| 3 | g·°C | 1 |
cm3 | 1 |
calorie | 1 |
kilowatt-hr | ||||||||||||
Problem 2: What is the formula in T2?
Problem 3: What units cancel out in the above calculations?
Problem 4: On the day you decided to heat the pool the water temperature was 8°C instead of 10°C. What cell above needs changed and what is the new value?

Problem 5: Since a watt is 1 joule per second, how many joules of energy is stored in all these batteries?
Problem 6: Also, if one horsepower is the same as 750 watts, how many minutes can I get from these batteries if I use a 10 horsepower electric motor?
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
| 1 | Total watt-hours from all batteries |
watt > joules/sec |
per second > per hour |
Total joules stored |
|||||||||
| 2 | 1200 |
watt-hours | 8 |
batteries | 1 |
joule/sec | 60 |
sec | 60 |
min | = |
???? |
joules |
| 3 | 1 |
battery | 1 |
watt | 1 |
min | 1 |
hr | |||||
| 4 | |||||||||||||
| 5 | Total watt-hours from all batteries | convert watts to horsepower |
convert to minutes |
factor in the 10 horsepower |
|||||||||
| 6 | 1200 |
watt-hours | 8 |
batteries | 1 |
horsepower | 60 |
minutes | 10 |
horsepower??? | = |
???? |
minutes |
| 7 | 1 |
battery | 750 |
watt | 1 |
hour | 10 |
horsepower??? | |||||

A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
T |
U |
|
Energy lost from the rocks |
equals |
Energy gained by the water | ||||||||||||||||||
| 1 | unknown specific heat |
mass rocks |
Final Temp |
Initial Temp |
specific heat water |
mass water | Final Temp |
Initial Temp |
||||||||||||
| 2 | - |
??? |
calories | g | °C | - |
°C | = |
1.00 |
calories | g | °C | - |
°C | ||||||
| 3 | g·°C | g·°C | ||||||||||||||||||
| 4 | Formula in I5 is "=D2*(F2-I2)" |
Formula in L5 is "=N2*(P2-T2)" | ||||||||||||||||||
| 5 | - |
??? |
calories | x |
calculated |
g·°C | = |
calculated |
calories | |||||||||||
| 6 | g·°C | |||||||||||||||||||
| 7 | Solving for unknown specific heat by dividing both sides by 58926 g·°C |
|||||||||||||||||||
| 8 | Formula in I8 is "=L8/L9" |
??? |
calories | = |
=L5 |
calories | Formula in L8 is "=L5" | |||||||||||||
| 9 | g·°C | =I9 |
g·°C | Formula in L9 is "=I5" | ||||||||||||||||
Problem 7: What is your answer for I5?
Problem 8: What is your answer for L5?
Problem 9: What is the specific heat of the rocks tested (I8)?
An electric blanket puts out about 100 watts of heat. Over 8 hours it puts out 100x8 or 800 watt-hours of energy. The common rock (quartz) has a specific heat of 0.19 cal/g·°C. Problem 10: How many pounds of quartz would have to be heated up to 450°C into order to give off the same about heat energy as the electric blanket if the rocks cool from 450°C (heated in a fire) to 37°C (body temp)? (These problems are difficult, but you just have to let dimensional analysis guide you. When I create problems like this, I don't know how to solve them initially. I just look at the units and decide what needs to get converted and let the dimensions guide the calculations. In the below spreadsheet I was getting some weird answers. I then realized Celsius units weren't canceling. I saw that the final and initial temps needed to be in the denominator for the Celsius in L2 to cancel. So, again, watching the units decides if multiplying or dividing is the right thing to do. Note: Subtracting 450°C from 37°C makes a negative number. Just treat it as a positive.)
A
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U | V |
|
| 1 | 100 watts for 8 hrs |
watt>joules/sec |
per sec > per hr (have joules at this point) |
joules>calories |
specific heat quartz: inverted |
Final temp |
Initial temp |
g>lb |
Total pounds rocks |
|||||||||||||
| 2 | 800 |
watt-hours | 1 |
joule/sec | 60 |
sec | 60 |
min | 1 |
calorie | g·°C | 1 |
lb | = |
???? |
pounds | ||||||
| 3 | 1 |
watt | 1 |
min | 1 |
hr | 4.18 |
joules | 0.19 |
calories | 37 |
°C | - | 450 |
°C | 454 |
g | |||||
Problem 12: What formula is put into U2?