FIRE and LIGHT:
Understanding the electronic structure of the atom began with a study of light. This picture with fire is appropriate because visible light is normally created by flames or something that is heated to high temperatures.

Understanding is Not Easy:
Understanding the nature of light and the nature of electrons
is not easy. One reason is we are almost as blind as a nearsighted fetus
with regards to seeing all light that is available. The nature of light
and electron structure can be confusing to the point where we feel we
might be too mentally limited to fully understand it.


Let’s say this image is made up of the whole electromagnetic spectrum. Roll the cursor over the image to see how much of the whole spectrum we actually see.
Yes, this is how blind we are. We are only picking up
about 1.5 percent of the picture that we could see if we could see the
whole electromagnetic spectrum.

Now assume this picture is just visible light, which it is. If we could see all the other frequencies of light, we could tell if he had a cellphone in his pocket because it would be flashing (radio frequencies). We could also see communication satellites in space (radio frequency). We could also tell the water had radioactive contamination from sparkles of gamma rays. We could see the train through the trees because the train would absorb radio waves. In the distance we could see that the ground was warm because of a fire put out 2 days ago. Basically, we could see 80 times more information than we do with our eyes.

Here is 1.5 % of the picture that represents the small amount that we see. Try to guess what it is.
Move cursor over the image to see the full image.


So even though we want to trust our eyes, we have to realize that they can fool us and are not giving us a complete image of what's around us.


We also notice how different materials reflect or absorb
colors.

FLAME TESTS:
Even powders that don’t have a color can produce flames with color. That means that heat is causing some elements to emit certain colors.
Different metals emit different frequencies of light. Of course our eyes may be seeing an orange flame but there may be other colors in the flame that we are missing. A prism would reveal that.

Flame Tests Analyzed:
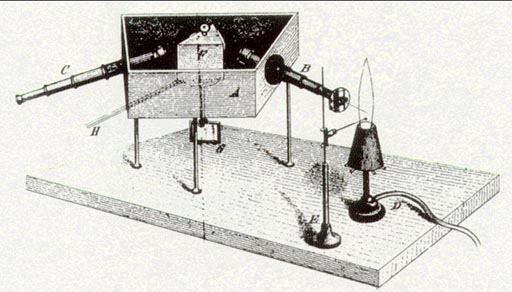
Gustav Kirchoff and Robert Bunsen realized that the flame tests might be a way to discover new elements.
SPECTROSCOPE:
Bunsen and Kirchoff invented a device (a spectroscope) that passed the light from the flame through a prism. That way could see all colors that a specific mineral was emitting. Bunsen invented the "Bunsen Burner" in order to get a clearer flame so it didn't interfere with the colors from the mineral in the flame. Bunsen burners have a opening at the bottom to let mix with the gas before it reaches the flame at the top. This premixing produces a cleaner and hotter flame.

Using this spectroscope, they discovered two new elements. One they called "rubidium" because it emitted a reddish light. "rubi" means red, which is also why ruby jewels are called rubies.
The other element discovered was cesium. Cesium emitted a blue light and was named after the Latin word, Caesius, meaning bluish gray.

Instead of a flame, one can put an element in a tube and heat it with electricity until it emitted light. If the light goes through a slit and then passes through a prism, the various frequencies of light emitted are separated into a spectrum. Our eyes can see the frequencies that are in the visible light range, but there are other frequencies of light emitted we can't see.


WAVE VOCABULARY:
By the way, the numbers on the spectra above are nanometers,
meaning "billionth" of a meter
(10-9 m). This leads us into wave vocabulary. The Greek letter, lambda,
represents the wavelength of light. Wavelength
is the distance from one peak to another peak. It is usually measured
in meters, nanometers, or angstroms (10-10 m). The Greek letter nu
(v) is used to represent frequency, which is
how many waves (cycles) are created per second.

WAVE CALCULATIONS:
Since light travels at the speed of light (represented by "c") the formula shown connects wavelength, frequency and the speed of light. Dimensional analysis confirms that the formula is correct. Wavelength (in meters per cycle) multiplied by frequency (in cycles per second) ends up as meters per second because cycle cancels out. Meters per second is a measurement of speed.

Let's do a problem. The laser that is used to attach a detached retina uses a beam with wavelength of 640.0 nm. That's a red color. If asked to calculate frequency, we use the formula (1). To solve for nu (frequency), we divide both sides of the equation by the wavelength lambda (2). We end up with a formula for frequency (3). The speed of light is 300,000,000 meters per second (3.00x108ms-1). Note: "s-1" means "per second". If you ever see "-1" by a unit of measurement, realize it's a short way of saying "per" and it allows you to put the amount in the numerator rather than the denominator. We plug in the speed of light and the wavelength (640 nm). Note: "n" (nano) will not cancel, so we multiply by "n" over 10-9. Remember, "n" and 10-9 are the same, so it's like multiplying by 1. The answer is 4.688x1014 cycles per second. Sometimes, books will leave out the word "cycles" and show the number just as "per second" (s-1)


A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | 91.5 Megahertz |
Speed of light |
||||||||
| 2 | =91.5*10^6 |
cycles | =3.00*10^8 |
meters | Ideal length is |
|||||
| 3 | second | second | half cycle |
|||||||
| 4 | 91.5 Megahertz Inverted |
Speed of light unchanged |
meter > ft |
Antenna ft. | ||||||
| 5 | second | =3.00*10^8 |
meters | 1 |
ft | = | 5.37 | feet | ||
| 6 | =91.5*10^6 |
cycles | second | 0.3048 |
meter | 2 |
half cycle | |||
What is the length in feet of the antenna best matched to 98.7FM? That would calculate out to be 0.499 feet.

Despite warnings from his friend, Phillip Von Jolly, Max Planck went into physics. Max started studying the relationship of temperature, color (frequency), and energy coming from material that absorbs & emits all light. They call it a black body since black absorbs light (and emits light). The most practical black body is a chamber that has a small hole in it.
The theory at the time predicted that the hot black body would produce a higher intensity of light at the higher frequencies of light (such as ultraviolet light) than lower frequencies. However, that wasn’t what the actual data showed.
To account for this, Max assumed that higher frequency light needed more energy, therefore reducing its chances of being created.

The formula for that energy was set to E=hv, where
v is the frequency and h is a conversion constant to turn frequency
in to energy. h is called Planck’s constant (after Max Planck). If we want answer in joules, the constant is
6.62606896(33)×10-34joule·seconds, which causes the seconds in "cycles per second" to cancel leaving joules of energy .
He also guessed that the electron oscillations making
light were restricted to whole number increments. For that reason, he
felt energy increased in increments. In other words energy might come
in a packet (a quantum). He didn't think people would believe him, so
he said this was just a mathematical fix and reality really wasn't like
that.

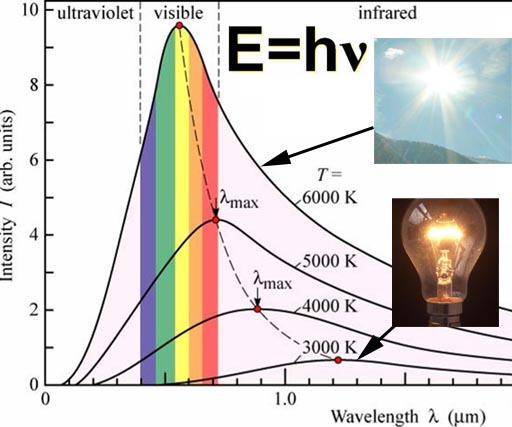
From this formula, the distribution of light can be graphed for different temperatures. Notice that that at 3,000 K, which is about the temperature of a standard incandescent light bulb, only about 5% of the light is in the visible range. Most of it is in the infrared region, which we feel as heat. So this kind of light bulb, is barely producing light, but mostly heat. So it's very wasteful, but has been the standard bulb for over 100 years.
At 6,000 K, which is the temperature of the Sun's surface, the peak color is yellow and there's a good production of visible light. Again, this is why our eyes have evolved to see this range of light. That's what the Sun produces the most of.
Another mystery at the time that seemed
unrelated, was the photoelectric effect.
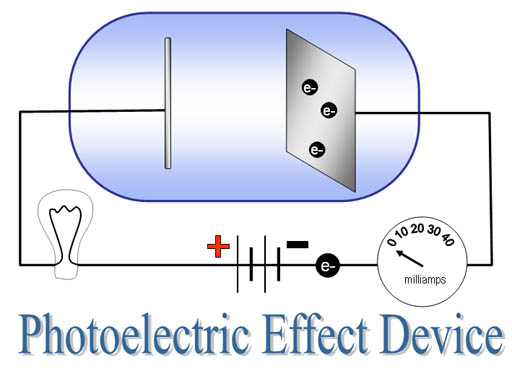
The device to illustrate the photoelectric effect was a plate and wire
inside a vacuum tube. The battery is arranged so that a negative voltage
is applied to the plate. No current is flowing because the voltage is
too low to cause the electrons to break away from the plate.
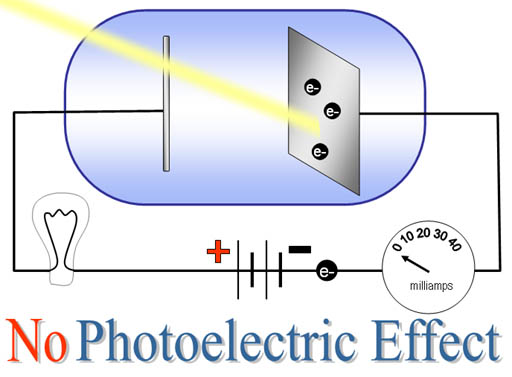
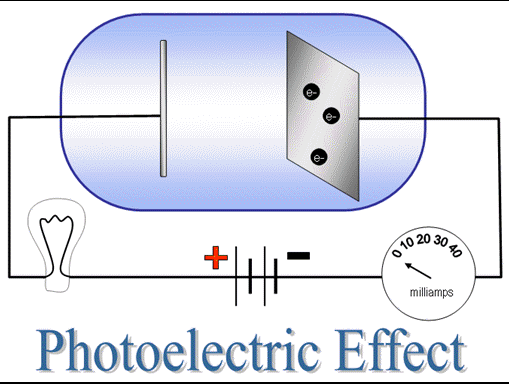
When ultraviolet light shines on the plate, electrons are ejected from the surface and current flows. (roll cursor over image to see animation) Electrons go to the other terminal and flow through the circuit. Other electrons leave the negative side of the battery and make it to the plate. If UV light continues, current will continue. At the time this effect could be demonstrated, but no one knew why UV light worked and visible light didn't.
This apparatus is often called a photocell or phototube.
It’s used to detect light. Instead of a sheet of metal, semiconductors
can be used. With small semiconductors as light detectors, one can make
video cameras or solar cells.

Here is a large phototube that is used to detect light. If the detector is metal, then UV light causes current to flow and can be detected. If made from a semiconductor (like computer chip material), then visible light will cause current and be detected.

The photoelectric effect also happens when UV light from the sun ejects electrons off of the moon dust. With electrons missing they become positively charged and start repelling each other. This causes the moon dust to fluff up and sometimes float a few feet above most of the moon’s surface.

Returning to the mystery. The mystery was how did light of higher frequency (UV light) eject the electrons? Einstein tackled the mystery by borrowing from Max Planck’s formula, E=hv.

Einstein proposed that light was not a continuous wave but a packet or particle of energy (later called photons). Energy could only transfer to an electron by being hit by one photon of light similar to the way one particle hits another particle. He knew that higher the frequency, the more energy these photons would have. Only when the photon’s energy was greater than the binding energy of the electron to the metal would an electron be ejected. (move cursor over image to see animation)

Light had been thought of as a continuous wave with energy
spread over the entire beam. Now with Einstein's explanation of the photoelectric
effect, light needed to be thought of as packets of energy or particles
of light (photons). The view of the universe changed because if energy
was in packets, that meant that time, distance, and about everything else
was broken down into packets. This required a huge rethinking of how we view the universe.



Someone asks how many photons of light are emitted by the laser? That seems like an impossible question to answer. Counting atoms is hard because they are so small. Photons are just as small and also traveling at the speed of light. However, by knowing the energy of each photon and the energy that the laser produces, we can count the photons. Dimensional analysis makes the calculation more certain. 2 watts means 2 joules (J) per second. By multiplying by 0.5 seconds, the seconds cancel and we have energy in joules (J). By taking our energy answer from above (1), we invert that so that joules cancel out. That gives us the final answer of 3.21x1018 photons.

A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
|
| 1 | E=hv or E=hc/?
|
||||||||||||
| 2 | (joules per photon) E= |
h=Planck's constant in Joules·seconds |
v=c/λ |
||||||||||
| 3 | 4.91x10-19 |
joules | == | =6.62606896*10^-34 |
J·s | =3.00*10^8 |
m/s | nano |
|||||
| 4 | 1 |
photon | 405 |
nm | =10^-9 | ||||||||
| 5 | |||||||||||||
| 6 | Power of laser |
Convert watts to joules/sec |
x blink time makes joules |
Divide by A3 | # Photons | ||||||||
| 7 | 6.00 |
milliwatts | 1 |
joule/sec | 0.001 |
350. |
milliseconds | 0.001 |
1 |
Photon | = | 4.28x1015 |
photons |
| 8 | 1 |
watt | milli |
milli |
=A3 |
Joules | |||||||
Why were E7 and E8 added to the calculations? These were to cancel the milli in milliwatts.
What is the formula in A3? The formula in the spreadsheet would be =D3*F3/F4/H4
What is the formula in L7? The formula in the spreadsheet would be = A7*E7*F7*H7/I8
A regular DVD uses 640nm laser and its power is 5.00 milliwatts. What cells in the spreadsheet would be changed in order to calculate the photons it creates in a blink of an eye? The cells to change would be F4 and A7

Let's now return to our mystery of the spectra of elements and how they might explain how the electrons in the atom are structured.


"n1" and "n2" are integers with n2 being larger than n1. Let n1=2 and n2=4. The formula says to square n1 (2x2=4) and to square n2 (4x4=16). These are put in the denominator and subtracted. 1/4 - 1/16. The answer is 3/16. That is multiplied by the Rydberg constant and then divided by both Planck's constant and the speed of light. The answer will be 1 over the wavelength. To get wavelength just take the answer and divide that into 1. The answer I get is 486 nanometers, which matches the light blue (turquoise) line in the spectrum. So now we have a formula that predicts the colors for hydrogen or any element that has just one electron, such as He+ or Li2+.
I don't know about you, but this is rather remarkable. This electron and the light it produces are obeying a formula that is just some simple fractions. Like I said, we live in a mathematical universe.
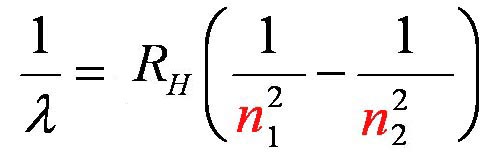
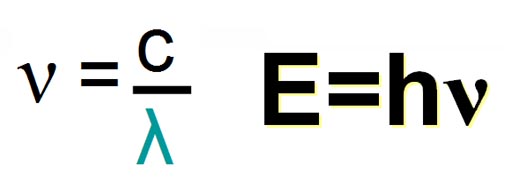

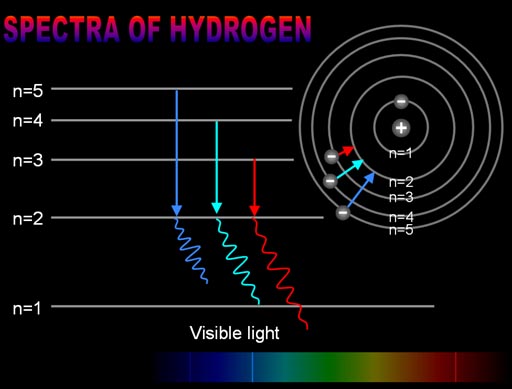
This image shows the energy jumps from the electron that produces these 3 colors. The highest frequency (dark blue) is produced when an electron drops from orbit 5 (n=5) down to orbit 2 (n=2). The turquoise blue (middle) is one we calculated earlier using the Rydberg formula. That electron drops from orbit 4 (n=4) down to orbit 2. The lower energy light (red light) happens when the electron jumps from orbit n=3 to orbit n=2.
What if an electron dropped from n=5 down to n=1?
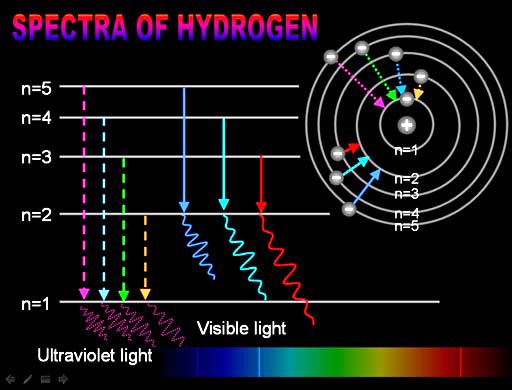
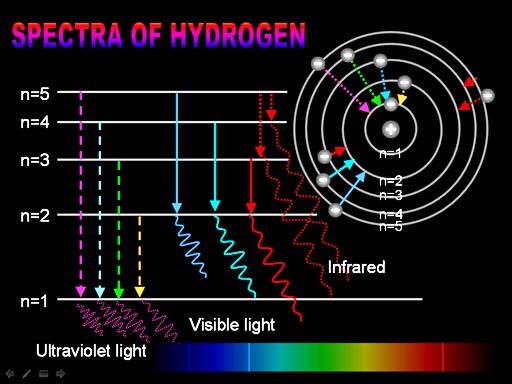
The only jumps we haven't mentioned are the little jumps from the higher "n" orbits. The n=5 to n=4 jump produces light at a lower frequency than red. It's infrared light. The n=4 to n=3 jump also releases infrared light. This is one reason the hydrogen lamp shown above will feel warm.
Note: There are higher orbits than n=5; however, the orbits get closer and closer. If an electron is pushed to higher orbits, it usually just escapes from the atom.
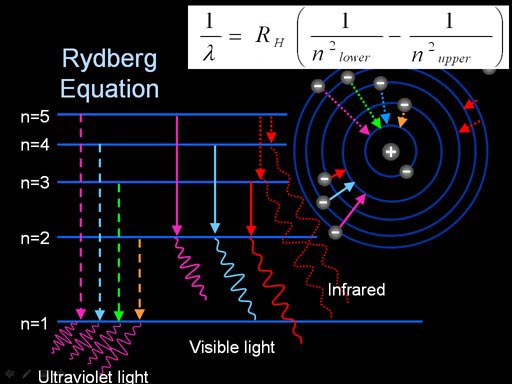
If any two "n" orbits are plugged into the Rydberg equation, all of these frequencies (wavelengths) can be calculated. As you should easily guess, I would use a spreadsheet to do the calculations.
Again, I think it amazing that we humans figured this out. Atoms are extremely small, but we are making progress in understanding what electrons are doing inside an atom by looking at its light and using mathematics. This is like understanding what is happening inside of car radio by just listening to the music. On top of that, doing that with a car radio that is so small that it's invisible.
A |
B |
C |
D |
E |
F |
G |
H |
I |
K |
|
| 1 | 1/λ (1/wavelength) |
Ryberg's constant |
2 |
=nlower |
3 |
=nupper |
||||
| 2 | 1 |
= |
10973731.6 |
m-1 | ( |
1 |
- |
1 |
) | |
| 3 | λ (meters) |
=E1^2 |
=G1^2 |
|||||||
| 4 | ||||||||||
| 5 | The above calculations solve for 1/λ. We want just λ. So below we put 1/λ in the denominator (cell C7). 1÷(1/λ)=λ (cells C6 & C7). Above and below, the m-1 means "per meter". For cell D2, the m-1 could have been placed in cell D3 as simply "m". The m-1 in cell D7 is moved to cell D6 and turned into simply "m" for meters. To make nanometers we multiply by nano over 10^-9. | |||||||||
| 6 | 1 |
nano |
= | 656 |
nm | |||||
| 7 | =C2*(1/F3-1/H3) |
m-1 | =10^-9 |
|||||||
| 8 | The above calculation gives 6.56x10-7 meters which then is converted to nm |
|||||||||
The above calculation was for an electron jumping from n=3 to n=2. What would be the wavelength of light emitted if an electron jumped from n=4 to n=2? In the above spreadsheet, 4 would go in cell G1 and 2 would go into cell E1. The formula in cell E3 would take the 3 and square it. So F2 and F3 become 1/4. The formula in cell H3 would take the 4 and square it. So H2 and H3 become 1/16. These and other calculations are done automatically and the new wavelength will show up in cell H6 as 486 (nm).
Regarding the light emitted in problem 9, what is its color? This is blue.
What would be the wavelength of light emitted if an electron jumped from n=4 to n=1? (This will be in the UV range). In the above spreadsheet, 4 would go in cell G1 and 1 would go into cell E1. The new wavelength will appear in cell H6 as 97.2 (nanometers), which is in the UV light range.
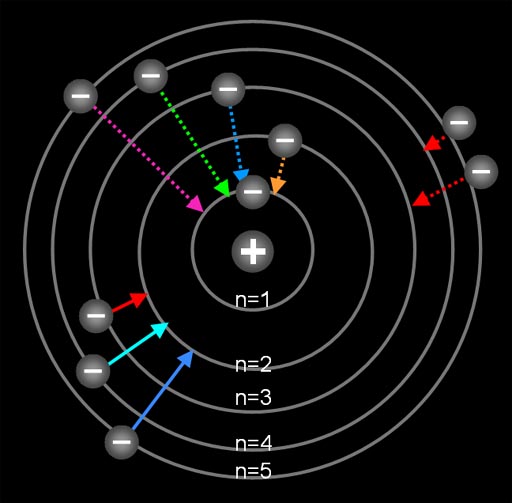
Realize that hydrogen has just one electron. These are the different orbits the electron can jump to if subjected to heat or light.
In the early 1900's this was the picture of the atom and the electrons.





Remember when I first introduced a joule, I said it was the energy used to push 1 liter of water (1 kilogram) across 1 meter distance so its speed would get up to 1 meter/sec speed in 1 second time. All those words become 1 kg·m2/s2

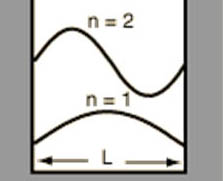
For a wave to be stable, its frequency much match the speed of its reflection. When that happens, the wave appears to be standing still. They call this a "standing wave."

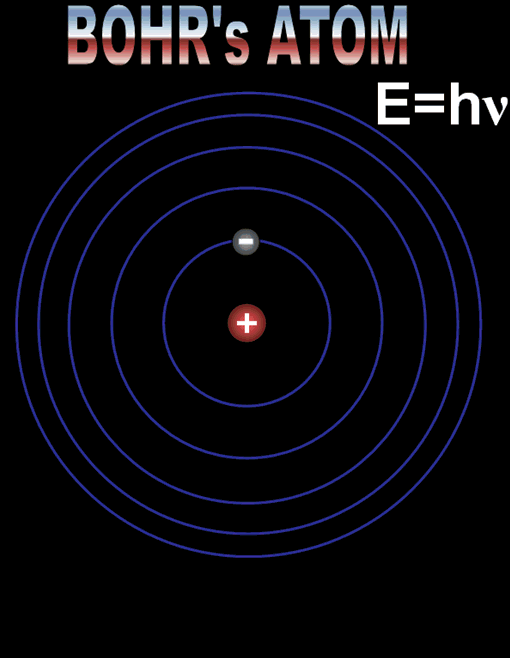
Bohr’s atom showed electrons as particles similar to planets going around the sun.
de Broglie’s atom treats electrons more as waves with wave patterns that fit symmetrically within the atom. In both cases, the energy levels of the electrons must go up by an incremental quantity (quantum).
Both of these played a role in the modern theory of the atom and the structure of the electrons. As the progression of elements were built by adding one proton and one electron at a time, the position of the protons was always in the center of the atom in the nucleus. However, electrons repelled each other, so as each electron got added for each new element, they would find a position and shape that maximized their distance from each other. Amazingly, the way they positioned themselves followed a fairly basic pattern.

In the sheet music shown, the F chord on the guitar is playing 4 notes. Are any of these notes being played with the G chord? (Hint: look at the fingering chords at the top. See if they have any common dots.) The is answer is no. These do not share any notes.
Are any of F chord notes played with the Bb (B flat) chord? The is answer is yes. The Bb chord has notes (dots) in the guitar chords that match. By the way these are F notes.
1, 4, 9, 16, 25, 36, ?
1, 3, 6, 10, 15, 21, ?
kilo (103), mega (106), giga(109), tera(1012), peta(10?)
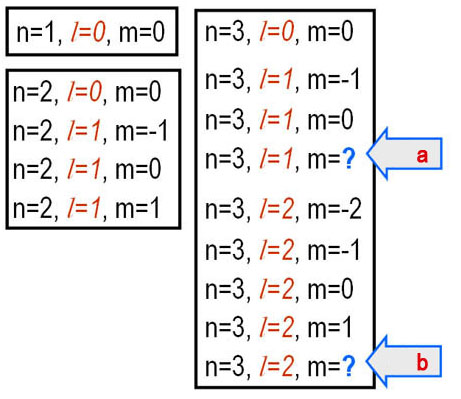
In the progression on the left, what numbers are "a" and "b"?
The answers to "a" and "b" above are +1 and 2.
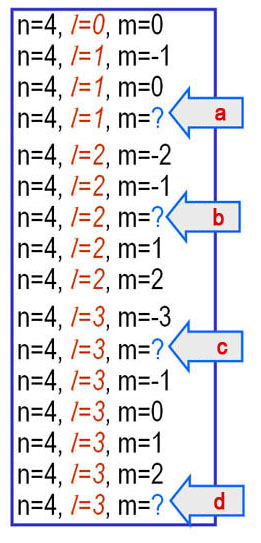
In the progression on the left, what numbers are a, b, c, and d?
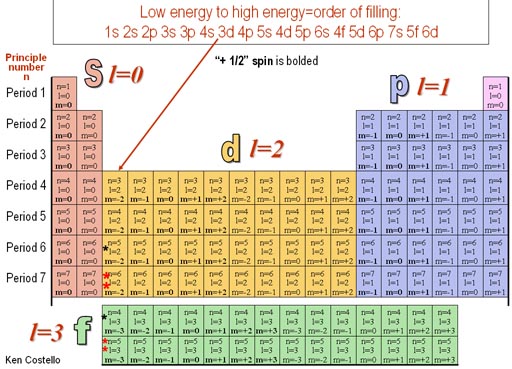
n=2, l=0, m=0, s=-1/2
n=2, l=1, m=-1, s=+1/2
n=2, l=1, m=-1, s=-1/2
n=2, l=1, m=0, s=+1/2
n=2, l=1, m=0, s=-1/2
n=2, l=1, m=1, s=+1/2
n=2, l=1, m=1, s=-1/2

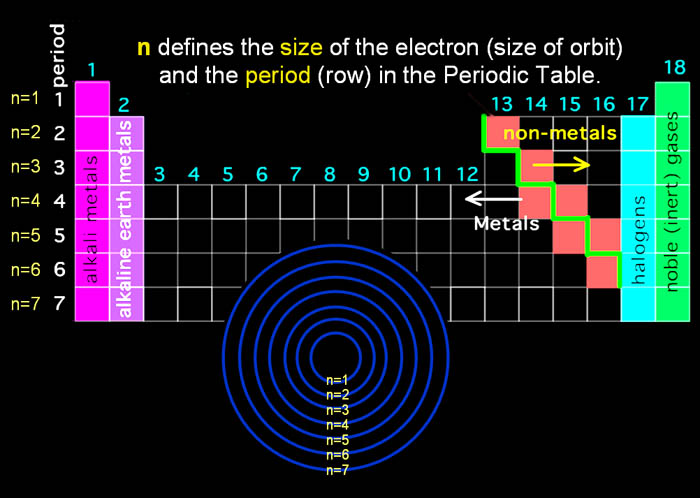
Again, "n" is the size of the electron and determines what period the element belongs in.
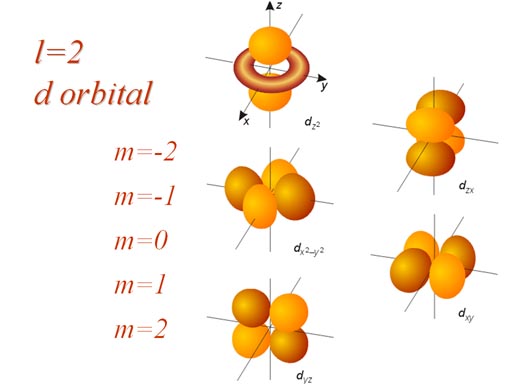
"l" determines the shape of the electron. For electrons that have l=0, it means their shape is spherical. If l=1, then the shape is dumbbell shape. If l=2, the shape has four lobes. If l=3, the shape has eight lobes. See below image. The "m" numbers represent orientation.
These sets of numbers are called the quantum numbers for that electron. "Quantum" implies a whole number progression. Notice there are no fractions. So the change of electron size, shape, and orientation does not happen gradually but in jumps, which is the essence of quantum chemistry (quantum physics).

As mentioned, the "l" value determines the shape of the region (or orbital) that the electron will most likely be found. These shapes (orbitals) were given letter names before the idea of quantum numbers were proposed. Below is how the orbitals got their names.
Before moving on, realize that electrons are not confined to these regions drawn. The shapes are the boundary where the electrons spends 90% of its time. 10% of its times its farther away.


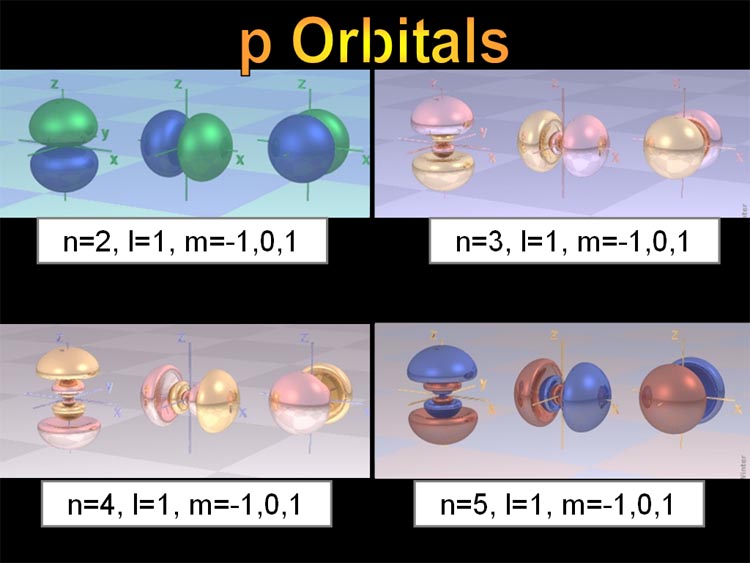

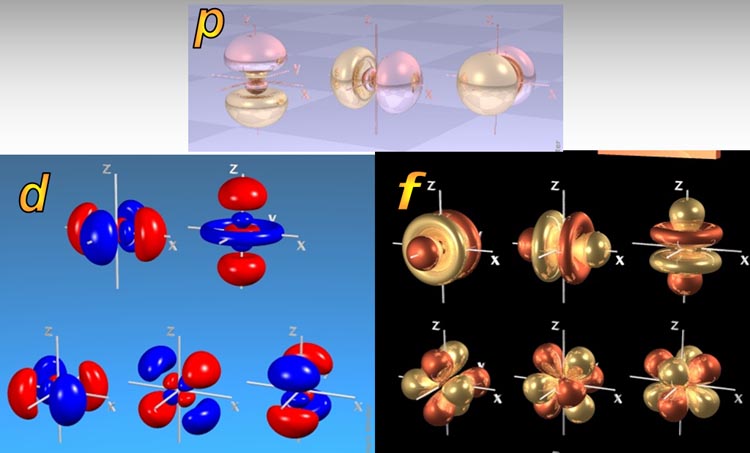
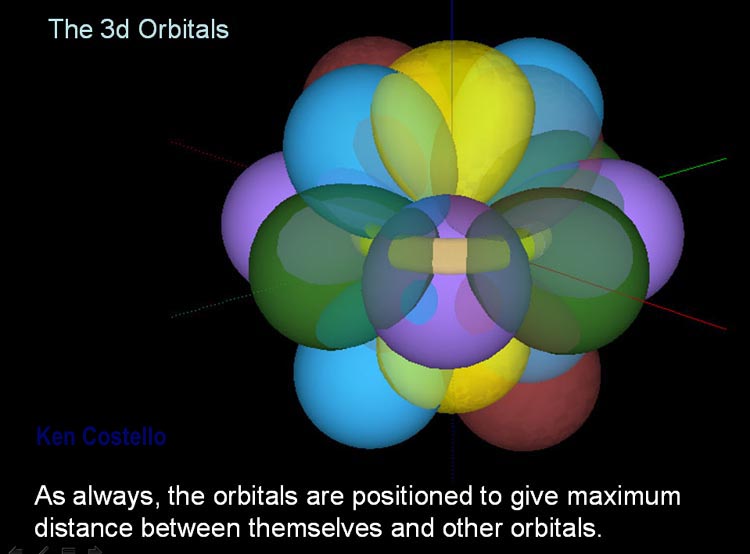
The above image is only showing 5 electrons. If each one is holding a pair of electrons with opposite spins, then the image could contain 10 electrons. Imagine gold with 79 electrons. Many of those are f orbital electrons, which are even more complex. So there's a whole whirlwind of activity in just one atom. I'd love to see an animation of that.
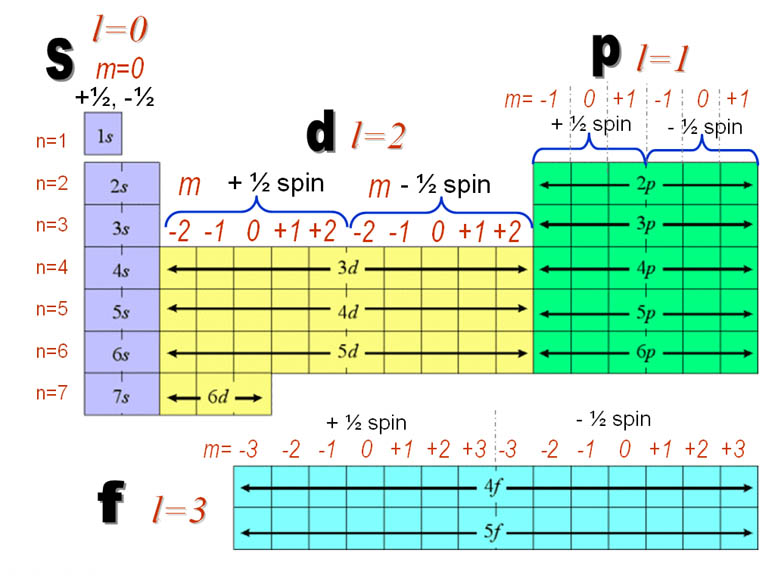
In the filling order at the top, the 4f orbital energy is just after 6s orbitals. That's why there's an indication on Periodic 6 column 3 "*", that the 4f orbital group comes next.

The road to get an understanding of the atom was not easy. It required a close look at the light that comes from flames and a brave rejection of the accepted ideas about nature.
We've learned that light is not continuous, that energy comes in packets and electrons behave as particles and waves. There's a simple view of electrons orbiting the nucleus and a wave view of them oscillating back and forth in certain regions according to a progression of values of n, l, and m. The motto I get from all this is that "Nothing is as simple as it looks and nothing is as complicated as it looks."


Here is a product that you add to the
fire in a fireplace, wood stove, or campfire. Notice that it has a warning
about being harmful or fatal if swallowed. It also probably isn't that
healthy to breathe either. A different ad for this product says it produces
blue and green colors (red and yellow are already present in wood fires).
Visit Wikipedia's article
on flame tests and see which elements might be used in this product
to produce blue, green, or blue-green flames.
http://en.wikipedia.org/wiki/Flame_tests
For more information and pictures of a fireplace with these colorglo crystals check out this webpage: