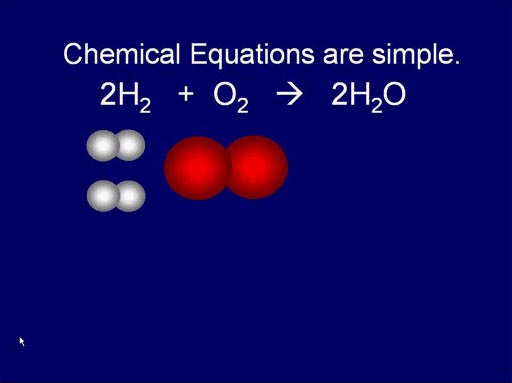
The Art of Counting without Counting

Stoichiometry comes from Greek "stoikheion" meaning element and "metry" from "metron" meaning to measure. So stoichiometry is about measuring the mass and number of elements involved in a chemical reaction.
Because atoms are so small we must count them without counting them. We can also weigh them without weighing them.
Simple Combinations:
As said before, when atoms combine to make molecules, they combine in simple ratios, such as 1:1, 1:2, 2:2, 3:1, etc. There are no fractions. So this makes our job of counting much easier.
Chemical
Equations are simple: As shown in the
tutorial on moles, atoms combine in simple ratios. That means the chemical
equations that show and balance the starting "reactants" and
ending "products" are fairly simple.
Here we see how hydrogen and oxygen (reactants) react and produce water.
It's a simple rearrangement.
Roll mouse over image to see animation.

In the tutorial on moles, we got into the art of counting atoms or molecules by knowing their weight in grams. In the tutorials on chemical equations, we learn about the types of chemical reactions (equations) and how to balance chemical equations. Now we want to put these two skills together.

Need for Water:
I like to do problems that involve survival. That way you've got a good reason to learn how to do these calculations.
Let's say you are planning an expedition into a desert and water will be critical. They say that a person needs about 1 gallon or 4 liters of water a day to stay alive.
You don't mind carrying extra water, but liquid water has its drawbacks...

Liquid water drawbacks:
If water is spilled, it will quickly be lost as it soaks into the sand.
If the water gets contaminated with poison, bacteria, or mold, it would be unsuitable to drink.
If open to the hot, dry air, it will evaporate.
In some areas, the value of water is so high that you risk being robbed of your water.
Therefore depending only on liquid water has many drawbacks.

Salt Hydrates as an answer:
Many salts have water bound to the salt molecule. For example, Epsom salt has the formula of MgSO4•7H2O. This formula indicates that each magnesium sulfate molecule has 7 water molecules around it. The water that is bound to it will not evaporate in the sun nor get contaminated with microbes or poisons.
If spilled on the ground, it can be scooped up and salvaged.
Robbers won't recognize it as a water source.
The water will come free from the salt when heated with a flame.
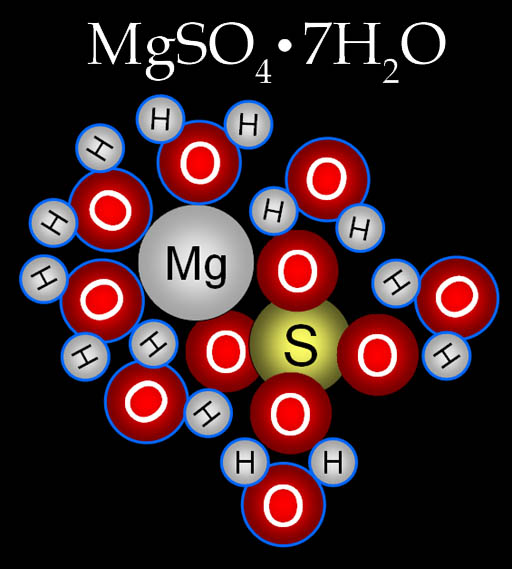
Here's the magnesium sulfate heptahydrate molecule. "Hepta" means "7" and "hydrate" means water.
When heated to 250°C, the water molecules are driven off. In a distillation apparatus, the water will condense and can be collected.
Now that we have a safe way to store some extra water,
let's get back to our expedition planning. We need 4 liters per day per
person. (Remember "per" is set up as a fraction. If you hear
"per" twice, then both are in the denominator and typically separated by a bullet "·".) Notice that
"persons" and "days" cancel (shown in red).
A |
B |
C |
D |
E |
F |
G |
H |
G |
|
1 |
Rate of water needed |
# persons |
# days |
||||||
2 |
4 |
Liters | 2 |
persons | 3 |
days | = |
24 |
Liters |
3 |
day · person | ||||||||
We need 24 liters of water. How many pounds of Epsom salts do we need to take with us in order for us distill off 24 liters of water?
When you hear a question that you have no idea how to answer, don't panic. You don't need to know how to do the problem right away. Just take it a step at a time.
You begin these kind of problems with a balanced chemical equation. This one is easy. The magnesium sulfate heptahydrate decomposes into anhydrous magnesium sulfate and 7 water molecules. "Anhydrous" means no water is attached to it.
MgSO4•7H2O -> MgSO4 + 7H2O
The problem would be easy if it asked "How many magnesium
sulfate heptahydrate molecules do you need to make 14 water molecules?"
From the balanced equation we see that there's one
magnesium sulfate heptahydrate molecule for every 7
water molecules.
14 H2O x 1MgSO4•7H2O
= 2 MgSO4•7H2O (1 is not written but understood)
7H2O
The thing to remember is that balanced equations are good at counting
the various molecules and seeing the ratio of one to the other. So that
means if we are given weight or volume, we must convert it to a number.
Moles is the preferred way to count these large numbers and because the
Periodic Table gives us weight per mole.

When dealing with water, it's easy to convert volume to weight. Once you have weight you can convert that to number (moles). Commit this to memory. A liter of water weighs 1,000 grams (1 kilogram).
We know we need 24 liters, so that's 24 kilograms or 24,000 grams.

The formula for water is of course, H2O. We refer to these sections of the Periodic Table to find the weight of each mole of hydrogen and oxygen. One mole of hydrogen weighs 1.008 grams. One mole of oxygen weighs 16.00 grams. For a mole of H2O, we need two moles of hydrogen atoms. So the total weight of a mole of H2O molecules is 1.008 + 1.008 + 16.00 = 18.016 grams.
Now we have a conversion for weight to moles.
A |
B |
C |
D |
E |
F |
G |
|
1 |
Water needed in grams |
Grams to mole conversion |
Water counted in moles |
||||
2 |
24000 |
grams H2O | 1 |
mole H2O |
= |
1332 |
moles H2O |
3 |
18.016 |
grams H2O | |||||
Now that we have moles of water we can use the equation to figure out
the moles of the magnesium sulfate heptahydrate. Looking at the equation we see the number of water molecules is 7 times that as the molecules of magnesium sulfate heptahydrate.
MgSO4•7H2O -> MgSO4 + 7H2O
A |
B |
C |
D |
E |
F |
G |
|
1 |
24 liters counted in moles |
Molecule ratio from balanced equation 1:7 |
MgSO4·7H2O counted in moles |
||||
2 |
1332 |
moles H2O | 1 |
MgSO4·7H2O |
= |
190.3 |
moles MgSO4·7H2O |
3 |
7 |
H2O |
|||||
In the spreadsheet the math formula put into F2 (the answer) would be: =A2/C3
That will divide the 1332 by 7 giving us 190.3. You don't have to multiply by C2 because that's just a "1".

We now know moles of Epsom salts, but the original question
is how many pounds of Epsom salts. Now we work backwards to find weight (mass).
To do that we need to know what one mole of magnesium sulfate heptahydrate
weighs. Just like water, we've got to go through the Periodic Table to
find the weight of one mole of each element in that compound.
MgSO4•7H2O

Here are the two sections of the Periodic Table that we can look up the mass of one mole of each of these atoms. Magnesium is 24.31 grams per mole. Sulfur is 32.07 grams per mole. Oxygen is 16.00 grams per mole, but since there are 4 oxygen atoms in sulfate and 7 in the 7 waters, that's 11 oxygen atoms. So 11x16.00g.=176g of oxygen in a mole of the compound. Hydrogen is 1.008 grams per mole, but there are 14 of them because there are 7 waters. Those all add up to 246 grams for each mole of magnesium sulfate heptahydrate.
This is how we changed grams to moles for water:
24,000 grams x 1 mole H2O = 1332
moles
18.016
grams
Above we show the the Epsom salt is 1/7 the number of water molecules (1/7 of 1332moles=190.3moles) Now we need to do the reverse. Change moles to grams for Epsom salt
190.3 moles x 246.5 grams MgSO4·7H2O = 46909
grams of Epsom salt
1 mole
Notice that to cancel the moles, gram is on top and mole
is on the bottom.

In the USA we don't normally buy things in grams but in pounds. So let's do one final conversion (grams to lbs).
Commit this number to memory. One pound is 454 grams. If you look at the bottom of the box, you will see that they say 1 lb. = 453 grams. It is actually 453.6 grams. So 454 is rounded up and 453 is rounded down. I remember 454 because my old Corvette had a 454 cubic inch engine.
46909 g. x 1 lb. = 103 lbs.
454 g.
So we have our answer. 103 lbs of Epsom salt will release 24 liters of water ( about 53 lbs of water).
Epsom Salt costs about $1 per pound, so for $103 we can help guarantee our survival.
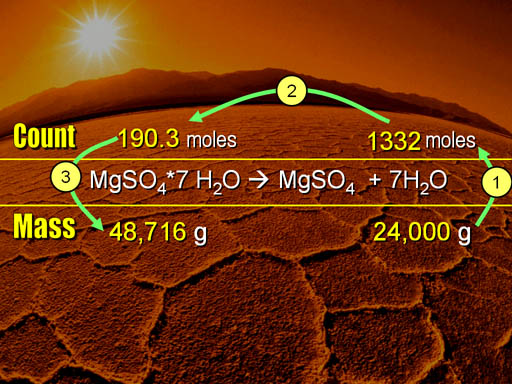
Here are the 3 steps that we followed. (1) We started with the 24,000 grams of water and converted that into the number of water molecules (1332 moles). (2) Using the 1 to 7 ratio in the balanced equation, we changed 1332 moles to 190.3 moles of magnesium sulfate heptahydrate. (3) That was converted to grams, and then to pounds.
With all of these calculations to do, you might prefer to just take your chances with the desert.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
|
1 |
4 liters of water per day
per person to survive |
24,000 g H2O at this point |
1332 mol H2O now | now 190.3 mol of salt |
now 46,909 g Epsom salt |
Now grams is in pounds. |
lbs to survive | ||||||||||||
2 |
#persons & days |
g/L of water |
g to moles H2O |
balanced equation |
mol to g for Epsom salt | conversion g to lb. |
Final lbs Epsom | ||||||||||||
3 |
4 |
Liters H2O | 2 |
persons | 3 |
days | 1000 |
g | 1 |
mol H2O | 1 |
mole MgSO4·7H2O | 246.5 |
g. MgSO4·7H2O | 1 |
lb Epsom salts | = | 103 |
lbs |
4 |
day · person | 1 |
L | 18.016 |
g H2O | 7 |
mole H2O | 1 |
mol MgSO4·7H2O | 454 |
g Epsom salts | ||||||||
The beauty of the above dimensional analysis setup is that you can change the number of persons or the days and the spreadsheet will calculate the new lbs of Epsom salts automatically. You don't have to go through all the steps again. In other words, once a spreadsheet is setup up, it can be used over and over with new input data. Also, instead of Epsom salts, you could find another hydrated salt and modify the molar mass to match the new hydrated salt and a new ratio to match the new balanced equation.
In earlier tutorials the strategy for many dimensional analysis problems was different than the one in the above spreadsheet. Earlier I said I like to do dimensional analysis problems that start with a fraction that best matches the answer. In this problem, we want pounds (lb) of Epsom salts. The only fraction in the above spreadsheet that has "lbs Epsom salts" is the conversion factor in columns O & P that converts grams to pounds. In this alternative method shown below, we start with that fraction because it matches the answer best. Then step by step we use related data to cancel out the units not wanted starting with "g Epsom salts". For example, C & D uses the molar mass of Epsom salts to cancel out the grams in cell B3 which we don't want.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
|
1 |
B2 matches answer. |
Using molar mass of Epsom salts, D2 cancels B3 |
Using ratio from balanced equation, F2 cancels D3 |
Using inverted molar mass of H2O, H2 cancels F3 |
Using 1000g per Liter of water, J2 cancels H3 |
Using water needs, L2 cancels J3 |
Using the 2 persons given, N2 cancels "person" in L3 |
Using the 3 days given, P2 cancels "day" in L3 | Final lbs Epsom salts |
||||||||||
2 |
1 |
lb Epsom salts | 246.5 |
g MgSO4·7H2O | 1 |
mole MgSO4·7H2O | 1 |
mol H2O | 1000 |
grams H2O | 4 |
Liters H2O | 2 |
persons | 3 |
days | = | 103 |
lbs Epsom salts |
3 |
454 |
g Epsom salts | 1 |
mol MgSO4·7H2O | 7 |
mole H2O | 18.016 |
g H2O | 1 |
Liter H2O | day · person | ||||||||
The above spreadsheets uses the same data as the previous spreadsheet except we begin with the fraction that has units that match our answer. That fraction will have some unit that is not in the answer. So we need to use data from the problem that will cancel out that unwanted unit (grams of Epsom salts in this case). The process is repeated until we only have the units of the final answer, which is lbs of Epsom salts. Notec that in both approaches we have counted molecules (in moles) of water and magnesium sulfate heptahydrate without actually counting them.
Reactant1 + Reactant2 → Product1 + Product2
The usual stoichiometry problem starts with you being given the mass (usually grams) for one of the reactants or products in the equation. You are then asked to find the quantity (usually grams) of one of the other reactants or products in the equation. The below three steps are one way to solve that problem.
1) Multiply the grams given of the one reactant or product by its molar mass (inverted molar mass actually), which turns the grams to moles.
2) Using the balanced chemical equation, convert moles of that reactant or product into moles of the reactant or product that is asked for.
3) Using the molar mass of the reactant or product asked for, convert its moles into grams.
The below spreadsheet shows the same steps but in spreadsheet format. The math is to multiply A2 x E2 x G2 / C3 / E3
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Grams given for one reactant or product |
Using the inverted molar mass, grams turns into moles |
Go from mole of one to moles of the other using ratio from balanced equation |
Molar mass of reactant/product in question turns its moles into grams |
Grams asked for |
||||||
2 |
given number |
grams of reactant/product | 1 |
mole reactant/product | varies |
mole reactant/product in question | from Periodic Table |
grams reactant/product in question | = | ??? |
grams of reactant/product |
3 |
from Periodic table |
grams reactant/product | varies |
mole reactant/product | 1 |
mole reactant/product in question | |||||
FACT: If the mass or moles of any compound is given, the mass or moles of any other compound in the balanced chemical equation can be found.
H2SO4 + 2NaOH → Na2SO4 + 2H2O
Above is a concrete example showing sulfuric acid being neutralized by sodium hydroxide (NaOH). Let's say we are given the mass of NaOH as being 5.00 grams. We are then asked how many grams of Na2SO4 (sodium sulfate) that will make. (Step 1) The first impulse you should always have when given grams is to get it converted to moles (get it counted) by multiplying by its molar mass. Use the Periodic Table. (Step 2) Once counted we look at balanced equation and see that the number of NaOH is twice the number of Na2SO4. (Step 3) Now we convert the moles of Na2SO4 to grams by consulting the Periodic Table and then we are finished
Let's go through the steps one by one.

First let's find the molar mass of sodium hydroxide (NaOH) by consulting the Periodic Table.
Na (sodium) is 22.99 grams per mole. Oxygen is 16.00,
and hydrogen is 1.008. Those add up to 40.00 grams per mole of NaOH. Note: Below we invert the 40.00 g/mole to be 1 mole/40.00 g because we need grams to cancel.
5.00 g. x 1 mole = 0.125 moles NaOH
40.00
g
Now for step (2), which is to convert moles of the starting compound into the moles of the compound in question. The balanced chemical equation shows that there are two molecules (or moles) of NaOH needed to produce one molecule (or mole) of Na2SO4.
| 0.125 |
x | 1 mol Na2SO4 | = 0.0625 moles Na2SO4 |
| 2 |
Note: "mol" is an abbreviation for "mole". Also note that "mol NaOH" gets cancelled.
Step (3) The last step is to convert the 0.0625 moles of Na2SO4
to grams. Consulting the Periodic Table above, we get 32.07 g/mol for
sulfur. 16.00 g/mol for one oxygen (multiply by 4 because it's O4) and 22.99 for Na (times 2). That
all adds up to 142 grams per mole of Na2SO4. By multiplying the moles of Na2SO4 times its molar mass, the moles cancel and we get grams of Na2SO4.
0.0625 mol x 142 g. = 8.88 g. Na2SO4
1
mol
Notice "moles" are placed so that they cancel. So 8.88 grams
is the final answer.
H2SO4 + 2NaOH → Na2SO4 + 2H2O
The above example was done in 3 steps. This can also be shown as one long calculation using dimensional analysis. Sometimes it's easier to see it all together. As usual, I prefer a spreadsheet to do and show calculations. Below are the 3 steps above as one long calculation. Notice the items with the same color text cancel:
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Starting grams given |
Turn g. NaOH to moles |
Ratio from balanced equation |
Molar mass turns moles Na2SO4 to grams |
Grams asked for |
||||||
2 |
5.00 |
grams NaOH | 1 |
mole NaOH | 1 |
mole Na2SO4 | 142 |
grams Na2SO4 | = | 8.88 |
grams Na2SO4 |
3 |
40.00 |
grams NaOH | 2 |
mole NaOH | 1 |
mole Na2SO4 | |||||
The above spreadsheet is one common way to solve these kind of stoichiometry problems. It begins with the starting quantity given for one compound and works its way to find the quantity of another compound. If the starting quantity were given in moles, then columns C & D would be eliminated.
In earlier tutorials the strategy for many dimensional analysis problems was different than the one in the above spreadsheet. One way I like to do dimensional analysis problems is to start with a fraction that best matches the answer. In the above problem, the answer is in "grams of Na2SO4". In columns G and H above, the molar mass has "grams of Na2SO4". So that would be the starting fraction for this other approach shown below. Note B2 is same as K2. In dimensional analysis the next step is to eliminate the units that are not in the answer. In the first step of this example, we need to eliminate "mole of Na2SO4" (cell B3). To do that we use the ratio of moles of Na2SO4 to moles of NaOH shown in the balanced equation. Now D2 cancels B3. Next we see cell D3 has moles of NaOH. We need to cancel that so we use the molar mass of NaOH. Finally we need to cancel out the grams of NaOH in F3. We use the starting quantity of grams of NaOH to do that. The only unit left is grams of Na2SO4
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Best match of units: Molar mass Na2SO4 |
Using data from balanced equation D2 cancels B3 |
Using inverted molar mass of NaOH F2 cancels D3 |
Using starting grams of NaOH H2 cancels F3 |
Only unit left is grams of Na2SO4 |
||||||
2 |
142 |
grams Na2SO4 | 1 |
mole of Na2SO4 | 1 |
mole of NaOH | 5.00 |
grams NaOH | = | 8.88 |
grams Na2SO4 |
3 |
1 |
mole Na2SO4 | 2 |
mole of NaOH | 40.00 |
grams NaOH | |||||
The above spreadsheet has the same data as the previous spreadsheet; however, the colored columns were rearranged because the strategy was different. Pick the one that you like best. In both approaches we are counting (in moles) without counting (by using molar mass data) and we are coming up with masses of other compound without weighing (using molar mass data).

Let's do another problem. We all know that a regular candle consumes oxygen when it burns; however, there is another kind of candle that generates oxygen when it burns. It's called an oxygen candle or chlorate candle. Some are used in aircraft to provide oxygen to passengers when they pull down their oxygen masks. These oxygen/chlorate candles are also used in submarines and for rescues where oxygen may be limited, such as in mines. In an oxygen candle, powdered iron is burned with sodium chlorate (NaClO3) provides the oxygen to burn the iron. However, there is extra oxygen left over in the reaction. Below is the reaction. Notice the reactants (sodium chlorate and iron) are solids (s) and the products, sodium chloride and iron(II) oxide are solids. But oxygen is a gas (g).
NaClO3(s) + Fe(s) → NaCl(s) + FeO(s) + O2(g)
A person at rest uses about 3.5 mL (milliliters) of oxygen every minute for each kilogram of body weight. I weigh 91 kilograms (200 lbs). So let's say in a plane emergency, it may take up to 60 minutes for the plane to get to a lower altitude where oxygen masks are no longer needed. How many grams of sodium chlorate and grams of iron does the oxygen candle need in order to keep me alive?
Note this is two questions. One is for grams of sodium chlorate and one for grams of iron.
Remember I've given two approaches for these kind of problems. One is to start with the quantity that is stated (given). In this case we are setting the oxygen quantity to the amount of oxygen I need to breathe for an hour. We then work our way to find the quantity (grams in this case) of what is asked (grams of sodium chlorate and iron). In previous problems we were given the grams of one of the elements/compounds in the equation. However, here we have to calculate it first. So the first spreadsheet below does that.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
||||
1 |
O2 consumption rate |
My mass |
Time to breath |
Volume to mole conversion for all gases (covered later in course) |
mole to grams |
cancel m in mL (B2) |
Grams of O2 that is set |
|||||||
2 |
3.5 |
mL | 91 |
kg | 60 |
min | 1 |
mole | 32 |
g O2 | 0.001 |
= | 27.3 |
grams O2 |
3 |
kg·min | 22.4 |
Liters | 1 |
mole O2 | milli |
||||||||
Now we can use the same setup that goes from one quantity to the quantity that is being asked for. The quantity of starting substance changes from grams to moles, then to moles of requested substance. Then its moles is converted to grams.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Starting grams given (stated) |
Using molar mass O2, turn grams O2 to moles |
Change moles O2 to moles NaClO3. Ratio from balanced equation |
Molar mass turns moles NaClO3 to grams |
Grams asked for |
||||||
2 |
27.3 |
grams O2 | 1 |
mole O2 | 1 |
mole NaClO3 | 106.44 |
grams NaClO3 | = | 90.8 |
grams NaClO3 |
3 |
32.0 |
grams O2 | 1 |
mole O2 | 1 |
mole NaClO3 | |||||
The other approach for calculating grams of NaClO3 is to start with a fraction that contains "grams of NaClO3". That would be the molar mass of NaClO3. Then we cancel the units not wanted one by one by using appropriate facts or data from the problem. Notice it's the same data/facts as in the above spreadsheet but the sequence and reasoning is different. Use whichever one seems more logical to you.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Best match of units: Molar mass NaClO3 |
Using ratio from balanced equation D2 cancels B3 |
Using inverted molar mass of O2 F2 cancels D3 |
Using starting grams of O2 H2 cancels F3 |
Only unit left is grams of NaClO3 |
||||||
2 |
90.8 |
grams NaClO3 | 1 |
mole NaClO3 | 1 |
mole O2 | 27.3 |
grams O2 | = | 90.8 |
grams NaClO3 |
3 |
1 |
mole NaClO3 | 1 |
mole O2 | 32.0 |
grams O2 | |||||
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Starting grams given (stated) |
Using molar mass O2, turn grams O2 to moles |
Change moles O2 to moles Fe Ratio from balanced equation |
Molar mass turns moles Fe to grams |
Grams asked for |
||||||
2 |
27.3 |
grams O2 | 1 |
mole O2 | 1 |
mole Fe | 55.854 |
grams Fe | = | 47.7 |
grams Fe |
3 |
32.0 |
grams O2 | 1 |
mole O2 | 1 |
mole Fe | |||||
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Best match of units: Molar mass Fe |
Using ratio from balanced equation D2 cancels B3 |
Using inverted molar mass of O2 F2 cancels D3 |
Using starting grams of O2 H2 cancels F3 |
Only unit left is grams of NaClO3 |
||||||
2 |
55.854 |
grams Fe | 1 |
mole Fe | 1 |
mole O2 | 27.3 |
grams O2 | = | 47.7 |
grams Fe |
3 |
1 |
mole Fe | 1 |
mole O2 | 32.0 |
grams O2 | |||||
Below are the same spreadsheets but they show the pattern of how the units are cancelled. The top one starts with the given units (B2=grams O2) and ends with the desired (asked for) units (H2=grams Fe). The bottom one starts with the desired units (B2=grams Fe) and ends up cancelling all other units. In both cases you only end up with the desired (asked for) units.
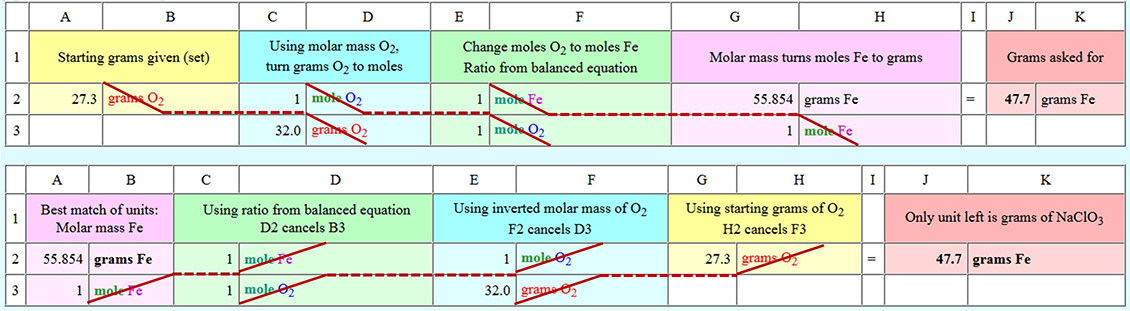
Regarding the amounts needed to keep me alive for one hour, we've calculated a need for a mixture of 90.8 grams of NaClO3 and 47.7 grams of powdered iron to make an oxygen/chlorate candle. The total volume of this mixture is only about 40mL. That's about the same volume of a ball point pen or 4 small birthday candles. So you see this mixture is an efficient (light weight and low volume) way to store and release oxygen.
C9H20(l) + 14O2(g) → 9CO2(g) + 10H2O(g)
The most common application of stoichiometry happens in your car's engine. The engine is constantly trying to mix the right amount of gasoline with the right amount of oxygen. Gasoline is a mixture of hydrocarbons with carbon chain lengths from 7 carbons to 11 carbons. That makes the average number of carbon atoms to be 9. So the average gasoline molecule would have this formula (C9H20). The above chemical equation represents the typical combustion reaction that is occuring in the engine's cylinders. To be stoichiometrically balanced, each molecule (or mole) of C9H20 requires 14 molecules (or moles) of O2. If there is less than 14 molecules (or moles) of O2, then there will be incomplete combustion and instead of the just carbon dioxide and water as products, you will end up with incomplete combustion and soot will be seen coming out of the exhaust. If there are more than 14 moles of O2 for each mole of C9H20, then the engine runs "lean" which means too little fuel (lean on fuel is same as excess of oxygen). That extra oxygen makes the combustion happen faster than normal. This can cause the gasoline/air mixture to explode before the piston has reached the top of the cylinder. That causes the piston to try to run backwards, which makes a knocking sound. That is bad for the engine and bad for power. This faster combustion also produces excess heat that can melt or degrade the piston. So the car's ECU (electronic control unit) works diligently with sensor data and the fuel injectors to keep the correct ratio of 14 molecules (moles) of oxygen mixed with 1 molecule (mole) of gasoline.
C9H20(l) + 14O2(g) → 9CO2(g) + 10H2O(g)
A simple stoichiometry question related to burning gasoline would be to ask how many grams of oxygen is needed to burn 12 grams (about a tablespoon) of gasoline? (The first spreadsheet below uses the approach of starting with the given grams (12 in this case). The second spreadsheets starts with the fraction that has units that match the answer, which is grams O2).
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Starting grams given (stated) |
Using molar mass C9H20, turn 12 grams C9H20 to moles |
Change moles C9H20 to moles O2 Ratio from balanced equation |
Molar mass of O2 turns moles O2 to grams O2 |
Grams asked for |
||||||
2 |
12 |
grams C9H20 | 1 |
mole C9H20 | 14 |
mole O2 | 32.0 |
grams O2 | = | 51.6 |
grams O2 |
3 |
104.2 |
grams C9H20 | 1 |
mole C9H20 | 1 |
mole O2 | |||||
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
1 |
Best match of units: Molar mass O2 |
Using ratio from balanced equation D2 cancels B3 |
Using inverted molar mass of C9H20 F2 cancels D3 |
Using starting grams of C9H20 H2 cancels F3 |
Grams asked for |
||||||
2 |
32.0 |
grams O2 | 14 |
mole O2 | 1 |
mole C9H20 | 12 |
grams C9H20 | = | 51.6 |
grams O2 |
3 |
1 |
mole O2 | 1 |
mole C9H20 | 104.2 |
grams C9H20 | |||||
In the above spreadsheets remember the data you need is the molar mass of the element or compound that has a known quantity and the molar mass of the desired (asked for) element or compound. You also need the ratio of the two as shown by the balanced equation and finally you simply need the starting (stated) amount. This data is arranged in a way to arrive at the desired units.

Real world problems are not as simple as the one just given. For example, your car engine can't weigh the grams of gasoline or grams of oxygen. It has to calculate the quantities indirectly. To find out how much oxygen is coming into the engine, cars utilize a sensor called the Mass Air Flow Sensor. It is tube shaped to allow the air from the car's air filter to pass through on the way to the engine. It has a heated wire that sits in the middle of tube so that air will pass around it. As the air passes around it, the heated wire cools. The amount of cooling is directly related to the mass of the air passing by. A signal (a voltage between 0 and 5 volts) is sent to the ECU (Electronic Control Unit) which can be translated into grams of oxygen per second.
C9H20(l) + 14O2(g) → 9CO2(g) + 10H2O(g)

This custom gauge has both a speedometer (top) and a tachometer (bottom). The tachometer indicates the motor is spinning at 4560 rpm (revolutions per minute). The 4560 revolutions per minute (RPM) is the same as 76 revolutions per second (4560/60=76). As the engine spins, the cylinders only draw air in every other revolution. So that means each piston draws in air 38 times (76/2) every second. Each time a piston draws in air, it needs a shot of gasoline to mix with that air so it can explode and produce power. So that's 38 firings per second. Or we can invert that and say there is 1 second per 38 firings.
If the Mass Air Flow sensor indicates 24 grams of oxygen is being pulled into the engine every second and this is connected to a 6 cylinder engine, how many grams of gasoline (C9H20) must be sent to each cylinder each time it fires (mixes with air and explodes)?
C9H20(l) + 14O2(g) → 9CO2(g) + 10H2O(g)
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
|
1 |
Rate of oxygen entering engine is given (stated) |
Using molar mass O2, turn grams O2 to moles |
Change moles O2 to moles C9H20. Ratio from balanced equation |
Molar mass turns moles of C9H20to grams of C9H20 |
Rate cylinders fire |
Grams needed for one firing in one cylinder |
||||||||
2 |
24 |
grams O2 | 1 |
mole O2 | 1 |
mole C9H20 | 104.2 |
grams C9H20 | 1 |
second | = | 0.0245 |
grams C9H20 | |
3 |
1 |
second | 32.0 |
grams O2 | 14 |
moles O2 | 1 |
mole C9H20 | 38 |
firings | 6 | 1 |
firing (in one cylinder) | |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
|
1 |
Molar mass turns moles of C9H20to grams of C9H20 |
Using ratio from balanced equation, D2 cancels B3 |
Using inverted molar mass of O2, F2 cancels D3 |
Using given rate of O2 entering engine,
H2 cancels F3 |
Using rate cylinders fire, J2 cancels H3 |
Grams needed for one firing in one cylinder |
||||||||
2 |
104.2 |
grams C9H20 | 1 |
mole C9H20 | 1 |
mole O2 | 24 |
grams O2 | 1 |
second | = | 0.0245 |
grams C9H20 | |
3 |
1 |
mole C9H20 | 14 |
moles O2 | 32.0 |
grams O2 | 1 |
second | 38 |
firings | 6 | 1 |
firing (in one cylinder) | |