An old and modern way of analyzing unknowns

A hundred years ago, chemists didn’t have much in the way of instruments that could analyze substances. They had a balance and a Bunsen burner. So the natural thing to do was to weigh something first, then burn it and then weigh the ashes.
If you started with plant material, the ashes would be minerals such as calcium carbonate, sodium chloride, potassium carbonate and more. Interestingly, the name potassium came from potash which is potassium carbonate. Water was poured over ashes and the salts that in the ashes were dissolved. That water was placed in iron pots and the water boiled away. The white residue was high in potassium carbonate know as "potash".
So let's say you had 100 grams of dry plant material and burned it, ant its ashes weighed 5 grams. So you can say that the plant material was 5% minerals.
You might learn that different kind of plants have a different percentage of minerals in them. So this kind of analysis could help you identify an unknown plant material. The tools to do this were simple—a balance and a fire.
C6H12O6 + 6O2 --> 6CO2 + 6H2O

MgSO4 + 7H2O --> MgSO4·7H2O (Epsom salts)
Let's say we weighed out 100.0 grams of glucose. The weight of the anhydrous MgSO4 powder before the glucose was burned was 110.0 grams. Afterwards, the powder weighed 169.3 grams. So that's an increase of 59.3 grams, which is from the absorbed water. We can turn the 59.3 grams of water to moles of water with our usual grams to mole factor.
59.3 grams H2O x 1 mole H2O = 3.29 moles H2O
18.02 grams
This counts the water molecules for us. For H2O, we see there are 2 hydrogen atoms for every H2O. So that means we have 2 x 3.29= 6.58 moles of hydrogen atoms. So we now know that 100 grams of glucose has 6.58 moles of hydrogen atoms in it, but this isn't enough to know its formula because we also need to know the number of carbon atoms and oxygen atoms. It's not easy to count oxygen atoms because when we burn the glucose, we are pumping more oxygen atoms into the chamber. However, we could measure the carbon atoms by measuring the CO2 that is released.

You may remember the Apollo 13 problem where you calculated how much CO2 two pounds of lithium hydroxide could absorb. Most hydroxides can absorb carbon dioxide. NASA likes lithium hydroxide because lithium is a very light metal. A cheaper hydroxide is lye (sodium hydroxide/NaOH). It's sold as a drain opener and also sold to those who make soap and biodiesel. Here's the equation for absorbing CO2:
2NaOH + CO2 --> Na2CO3 + H2O
The NaOH turns into sodium carbonate (washing soda). This process also produces water, which raises a problem. If we absorb the CO2 first, there will be water produced that will throw off our measurement of water in the canister of MgSO4 that absorbs water. So we have to place the NaOH canister after the MgSO4 canister.
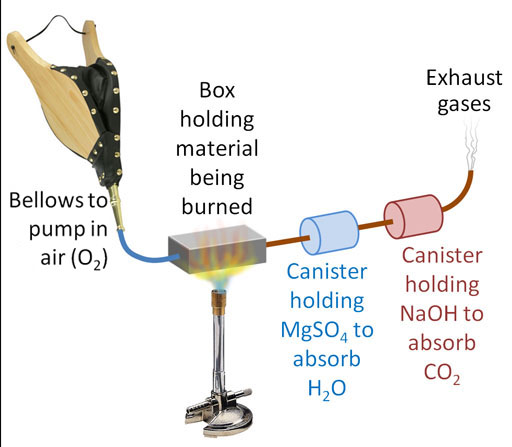
Here's our setup. We have two canisters. The first is to capture the H2O coming from the hydrogen atoms in the glucose. The second canister is to capture the CO2 which is coming from the carbon atoms in the glucose. Our plan is to burn 100.0g of glucose again, but first we have to know the starting weights of the MgSO4 and the NaOH. It doesn't matter if we know the starting weight of these powders or the starting weights of the canisters that hold these powders. We are only interested in the difference in weight from before and after the glucose is burned. So let's say the MgSO4 canister starts off weighing 223.4 grams and after glucose is burned it weighs 282.8 grams. That's a difference of 59.4 grams (similar as to before). The NaOH canister started with a weight of 155.2 grams and then after the burn, it weighed 241.8 grams. That's a difference of 86.56 grams.
C?H?O?
Using the above measurements and the power of math, we will come up with a formula for glucose. As usual we can't count atoms, but we can measure their mass. Here we have measured the mass of water absorbed by measuring the before and after weights of the MgSO4 canister. Then we can convert that to a count of hydrogen atoms:
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
1 |
MgSO4 canister |
|||||||||
2 |
End mass |
282.8 |
g | There are 2 hydrogen atoms per H2O |
||||||
3 |
Start mass |
223.4 |
g | |||||||
4 |
Water absorbed |
59.4 |
g H2O | 1 |
mole | 2 |
H | = |
6.60 | moles H atoms |
18.02 |
grams | 1 |
H2O | |||||||
The increase of mass in MgSO4 canister is just from H2O. However, the NaOH canister's increase in weight is from CO2 absoption but some mass from the original NaOH is lost as water vapor.
2NaOH + CO2 --> Na2CO3 + H2O
The canister's start weight was from the canister itself plus an unknown mass of the NaOH inside. The end weight was the canister itself plus an unknown amount of NaOH and an unknown amount of Na2CO3. Even though in chemistry we don't have to use algebra that often; this is one of those times that we do. (The below algebra is not something you will have to do in this class, but it shows the usefulness of algebra).
Let N be the starting grams of NaOH. Let C be the canister's weight. So the beginning canister's weights is C+N. Let S be the grams of Na2CO3 created. Let M be the grams of NaOH that got converted.
Canister after glucose burned: 241.8 g = C + N + S - M
Canister with NaOH start weight: 155.2 g = C + N
Subtracting the the start weight from the end weight: 86.6 g=(C+N+S-M) - (C+N) = S - M
This shows that the difference in weight is the grams of Na2CO3 created minus the grams of NaOH converted.
The number of grams of Na2CO3 created is the number of moles of Na2CO3 created times the 106 grams per mole that it weighs.
Let Y = moles of Na2CO3 created.
S=Y moles of Na2CO3 x 106 g/mol
From our equation: 2NaOH + CO2 --> Na2CO3 + H2O the moles of NaOH is twice that of the moles of Na2CO3 created. So moles of NaOH consumed is 2Y. So the grams of NaOH consumed is as follows.
M= 2Y moles of NaOH x 40.0 g/mol
Earlier we showed the the 86.6grams = grams Na2CO3 created minus the grams NaOH converted. We now have another way to write that:
86.6 g =Y moles of Na2CO3 x 106 g/mol - 2Y moles of NaOH x 40.0 g/mol
Moles cancels and the "2Y x 40" becomes 80Y, so the above simplifies to
86.6 g=106Y-80Y
86.6 g=26Y
Solving for Y
86.6 g = 26Y
26 26
Y=3.33 moles of Na2CO3
There is one carbon for each molecule of Na2CO3, so that means there are also 3.33 moles of carbon in this 100.0g sample of glucose. Earlier we showed that there was 6.60 moles of hydrogen in the glucose sample. Glucose also has oxygen in it, so how is that measured? We don't have to. We can subtract the grams of carbon and hydrogen from the 100.0 grams, and oxygen will be the remaining grams.
3.33 moles of carbon x 12 g/mol = 39.96 grams. 6.60 moles of hydrogen x 1.01= 6.666 g. So these total 46.6 grams. So that means that oxygen in the 100.0grams of glucose must be 100.0g-46.6g or 53.4grams.
Now we can get a count of the oxygen atoms.
53.4 g x 1 mole = 3.34 moles oxygen
16 g
Now we are almost there. We now have a count of all 3 elements. We can write our formula as:
C3.33H6.60O3.34
Normally, we don't see a mixed fractions in the subscript. So the way to fix that is to divide by the smallest number. The smallest is 3.33. So dividing that into all of these, we get these numbers: 1, 1.98, 1.003. Atoms don't combine as fractions. So the slight departure from a whole number is just the error in measurement of the weights of the canisters or not capturing 100% of the elements. So the final formula would be:
CH2O
A weakness of this technique of finding the formula is that we don't know if the molecule of glucose is just the 4 atoms in CH2O or is a multiple of this formula. In other words, it could be C2H4O2 or C3H6O3, C4H8O4, C5H10O5, C6H12O6, and so forth. The formula CH2O is called an empirical formula because it is supported by experiment data (empirical data) but it hasn't been proven as the formula for the real molecule of glucose. Other types of experiments are needed to show that its actual formula is 6 times the empirical formula of CH2O which is C6H12O.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
1 |
NaOH canister |
|||||||||
2 |
End mass |
241.8 |
g | There are 2 hydrogen atoms per H2O |
||||||
3 |
Start mass |
155.2 |
g | |||||||
4 |
Difference |
86.6 |
g | 1 |
mole H2O | 2 |
H | = |
6.60 | moles H atoms |
18.02 |
grams H2O | 1 |
H2O | |||||||

Many compounds also have nitrogen in them, such as amino acids, proteins, drugs, plant extracts, and more. So another trap is added to capture any nitrogen that is in the molecule. Again, because the sample is burned, the nitrogen is in the form of nitrogen oxide (NO). The same technique is used to measure the before and after weights of the canisters. With three canisters, empirical formulas for compounds that contain carbon, hydrogen, nitrogen, and oxygen can be determined.

Instruments that capture C, H, and N are often referred to as a Combustion CHN Elemental Analyzers. Remember they also find oxygen by subtracting the mass of C, H, and N from the sample mass to find the oxygen's mass. Instruments like these make the job much easier.

Here's another CHN analyzer. On the top is an automatic sample feeder. It can do a hundred or more analyses one after another. From the calculations you saw above, these analyses can be tedious, but instruments like this can make it a lot easier.
These instrument can analyze a very small sample. They say about 1 to 3 milligrams. That's hardly visible.

Here's a third type of CHN analyzer. This one can capture sulfur dioxide, so it can be used with compounds that have sulfur in them. Some elemental analyzers can also analyze for halogens (F, Cl, I, Br). The old elemental analysis methods required weighing the before and after weights of the canisters manually. The new ones do this automatically and then give a readout of percent of each element by weight. To get the actual molecular formula, other experiments need to be done to find the molar mass (the mass of one mole of the substance).
If the compound can be turned into a vapor, the volume, mass, and temperature of the vapor can be measured and from that the molar mass can be determined. That coupled with the elemental analysis can let you turn the empirical formula into its true molecular formula.
So let's do some problems that find the molecular formula using this type of data.

A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
|
1 |
Readout (mass%) |
Take % of 100g | grams to moles |
moles in 100 g |
divide by smallest |
make integer |
g/mol empirical formula |
|||||||||||||
2 |
Chlorine |
71.66% |
71.66 |
grams | 1 |
mole | = |
2.02116 | moles Cl | ÷ |
2.02082 |
= |
1.00 |
1 |
1 |
35.45 |
g | = |
35.45 |
g. |
3 |
35.45 |
grams | 1 |
mole | ||||||||||||||||
4 |
Carbon |
24.27% |
24.27 |
grams | 1 |
mole | = |
2.02082 | moles C | ÷ |
2.02082 |
= |
1.00 |
1 |
1 |
12.01 |
g | = |
12.01 |
g |
5 |
12.01 |
grams | mole | |||||||||||||||||
6 |
Hydrogen |
4.07% |
4.07 |
grams | 1 |
mole | = |
4.0377 | moles H | ÷ |
2.02082 |
= |
2.00 |
1 |
2 |
1.008 |
g | = |
2.016 |
g |
7 |
1.008 |
grams | mole | |||||||||||||||||
8 |
Empirical formula = Cl1C1H2 or ClCH2 |
grams per mole | 49.476 |
g | ||||||||||||||||
9 |
Molar mass of compound |
98.96 | g/mol | = |
2 |
x | Cl1C1H2 | = Cl2C2H4 | ||||||||||||
10 |
Mass of 1 mole of Empirical formula |
49.476 | g/mol | Actual Molecular formula | ||||||||||||||||
1. The percentages are turned into grams (columns C,D). The 100 grams is just arbitrary sample size that makes the calculations easier.
2. The grams of each element is turned into moles (columns E,F,G,H,I) Now we have them counted in moles.
3. To scale this count so that the smallest number is "1", we divide by the smallest number of moles, which here is 2.02082 (columns J,K,L,M). We round the numbers to 3 signficant figures because C6 has 3 significant figures. Atoms combine in whole numbers, so here we see that the 1.00, 1.00, and 2.00 are actually just 1, 1, and 2. Sometimes, they won't all be integers when rounded to 3 sig figs. If that happens, you have to do trial and error of multiplying all of them by 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, etc, until all of them are integers when rounded to 3 sig figs. Put the final integers into column O. This gives us the empirical formula (smallest size). In the example above, the numbers in column M were integers, so just multiplying by 1 was all that was necessary. However, if any of the values in column M had a fraction, you would need to find a multiplier (column N) to make it a whole number.
4. Use the empirical formula plus the atomic masses of each element in the formula to find the molar mass of the empirical formula (columns O,P,Q,R,S,T).
4. By knowing the mass of one mole of the actual compound, we can see if the empirical formula is the actual molecular formula or if we need to multiply that formula by some integer. In this case the actual compound's molar mass is twice the size of the empirical formula's molar mass (columns A,B,C,D,E,F). That means our empirical formula is only showing half the number of atoms that we should have. So by multiplying by two we get the actual molecular formula (columns F,G,H,I).
