1. Calculate the molarity of a solution prepared by dissolving 0.600g of KHC8H4O4 in enough water to make 50.0 mL of a solution.
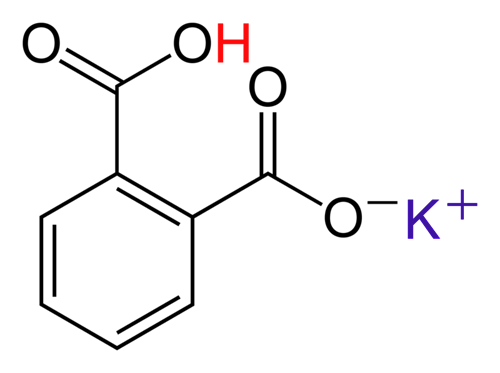
KHC8H4O4 is potassium hydrogen phthalate. The word "hydrogen" is referring the the acidic hydrogen. This hydrogen comes off to neutralize the any OH- ions. In the image below a potassium ion has replaced a hydrogen. Before the hydrogen was replaced, the molecule was called phthalic acid.
Molarity is moles per liter. Here you are given grams and milliliter. It is common to be told the grams of a substance because that's what you can measure out on a balance. You can't measure out moles. However, moles per liter (molarity)is a desired concentration because you have a count of the molecules that are in the solutions. As you know, chemical reactions are balanced by the number (the count or moles) of the reactants not their grams. So converting grams to moles is often done.
KHC8H4O4 (KHP) is a solid acid that doesn't absorb water, so it's easy to get an accurate weight and therefore useful in creating a known solution of an acid.
Practice for #1: 5.378 grams of KHC8H4O4 (KHP) is placed in 500 mL volumetric flask (accurate to 4 significant figures or 500.0 mL). What is the molarity of the KHP?
Remember liquid concentration is mass (or moles) divided by volume.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
| 1 | mass KHP |
grams>moles |
divide by volume |
cancel m |
molarity KHP |
|||||
| 2 | 5.378 |
g | 1 |
mole | m |
= |
0.05267 |
moles | ||
| 3 | 204.2220 |
g | 500.0 |
mL | 0.001 |
Liter | ||||
Below is the equivalent of the spreadsheet:
Note this answer has 4 sig figs. For problem 1, your answer should be in 3 sig figs. You can find the molar mass of KHP by looking up the molar mass of all of the atoms and adding them up. There are some websites that let you type in the formula and it will calculate the molar mass for you. One site is http://www.webqc.org/mmcalc.php, but they have a lot of advertising. Perhaps, another can be found that doesn't have adverstising.
2. Calculate the molarity of a solution prepared by dissolving 0.600g of H2C2O4•2H2O in enough water to make 50.0 mL of solution.
This problem is just like #1. So use Practice #1 as a guide. Remember to round your answer to 3 sig figs.
The problem doesn't identify what H2C2O4•2H2O is. It's useful to let a search engine like Google do a search on this formula to find out what it is. Results of the search find that it matches oxalic acid dihydrate. That used in rust removers and other strong cleaners. If a little gets in the mouth, it causes a lot of pain and the throat will close, and you won't be able to speak to let others know you are in trouble. The Dumb Cane contains a calcium salt of oxalic acid. If you chew on its leafs, needles of calcium oxalate will shoot into your mouth causing your throat to swell so you can't talk (dumb as in deaf and dumb).
3. If 30.65 mL of Ca(OH)2 solution is needed to react with 0.240 g of primary standard H2C2O4•2H2O, what is the molarity of the Ca(OH)2 solution?
__Ca(OH)2 (aq) + __ H2C2O4•2H2O (s) --> __CaC2O4 (s) + __H2O (l)
To find out the molarity concentration of the Ca(OH)2 solution, you first need to balance the neutralization reaction of calcium hydroxide with oxalic acid dihydrate. This forms calcium oxalate plus water.
__Ca(OH)2 (aq) + __ H2C2O4•2H2O (s) --> __CaC2O4 (s) + __H2O (l)
It's helpful to keep track of the acidic hydrogens (H+) on the oxalic acid and the hydroxides (OH-) in calcium hydroxide. The below equation shows the acid hydrogens in red and the hydroxides ion (OH-) in blue. Water is written as HOH to see that one hydrogen (H+) came from oxalic acid and the OH- came from calcium hydroxide. Also, a second water is written in green to show the water that comes from the dihydrate (2H2O).
__Ca(OH)2 (aq) + __ H2C2O4•2H2O (s) --> __CaC2O4 (s) + __HOH (l) + __H2O (l)
When balancing, it helps to start with the most complicated looking compound, which would be the oxalic acid dihydrate. If we have one of these molecules, then we get 2 (H+) ions and 2 water molecules coming off. Also, there will be one oxalate ion (C2O4)2+ . That makes the chemical equation look like this:
__Ca(OH)2 (aq) + H2C2O4•2H2O (s) --> CaC2O4 (s) + 2HOH (l) + 2H2O (l)
As we turn attention to the number of Ca(OH)2 molecules, we see that it has one calcium ion which is accounted for on the right side of the equation. It also has two (OH-) ions which are accounted for in the 2 waters on the right side. So the number in front of Ca(OH)2 is just 1, which is not written. We can now combine the 3 water molecules and simply write 3H2O.
Ca(OH)2 (aq) + H2C2O4•2H2O (s) --> CaC2O4 (s) + 3H2O (l)
This is the balanced equation. It shows the number of molecules (or moles) of calcium hydroxide matches that of oxalic acid dihydrate. Meaning that when we you moles of oxalic acid dihydrate using the mass of 0.240 grams given, that you are also finding the moles of calcium hydroxide being neutralized. To do the calculations, let the practice problem guide you.
Practice for #3: If 57.12 mL of Ca(OH)2 solution is needed to react with 0.956 g of primary standard H2C2O4•2H2O, what is the molarity of the Ca(OH)2 solution?
Titration problems must have one known amount that is used to find the unknown amount. Here we know the grams of the primary standard of oxalic acid dihydrate. Oxalic acid dihydrate can be a primary standard because it has already absorbed water, so its weight won't go up by absorbing water from the air. On the other hand, anhydrous (no water) oxalic acid would not make a good primary standard because it would be constantly absorbing water out of the air making it impossible to get an accurate weight. So the strategy is turn the 0.956 grams into moles of oxalic acid dihydrate, and then using the balanced equation to turn that into moles of calcium hydroxide. Since we want moles per liter (molarity), we need to divide the volume (mL) of the calcium hydroxide. See below spreadsheet for the setup. The answer is in 3 sig figs because the mass was only 3 sig figs.
A |
B |
C |
D |
E |
F |
G |
H |
I |
K |
L |
M |
|
| 1 | Mass of oxalic acid dihydrate |
mass to moles for oxalic acid dihydrate |
mole ratio 1:1 from balanced equation to get moles Ca(OH)2 |
Divide by volume to get concentration |
cancel "m" to get just Liters |
molarity of Ca(OH)2 |
||||||
| 2 | 0.956 |
g |
1 |
mole H2C2O4•2H2O | 1 |
mole Ca(OH)2 | m |
= |
0.138 |
moles | ||
| 3 | 126.066 |
g | 1 |
mole H2C2O4•2H2O | 57.12 |
mL | 0.001 |
L | ||||
4. If 41.40 mL of 0.1283 M NaOH solution is needed to neutralize 50.00mL of an H2SO4 solution, what is the molarity of the H2SO4 solution?
__NaOH (aq) + __H2SO4 (aq) --> __Na2SO4 (aq) + __H2O (l)
The strategy is to find the moles of NaOH using NaOH molar concentration and NaOH volume. Then using the balanced equation, you will see how many moles of NaOH are needed to neutralize a mole of H2SO4. Moles of H2SO4 divided by its volume will get you its molarity. First let us balance the above equation. Like before, it is more clear if you change H2O into HOH so that you can see the hydrogen that comes from the sulfuric acid.
__NaOH (aq) + __H2SO4 (aq) --> __Na2SO4 (aq) + __HOH (l)
We can start with balancing sulfuric acid. The 2 hydrogens in H2SO4 will end up providing the H+ ions to make water. That means we need a "2" in front of HOH in order account for the 2 H+ ions. By making it 2HOH, that causes us to need two OH- ions. So we look at NaOH and realize it needs a 2 in front of it. The number of sodium (Na) atoms and the sulfate ion (SO4)2- are balanced because we got the others balanced.
2NaOH (aq) + H2SO4 (aq) --> Na2SO4 (aq) + 2HOH (l)
The balanced equation tells us it takes 2 NaOH molecules to neutralize just one H2SO4 molecule.
Practice for #4: Battery acid in typical car batteries should have a molar concentration of 4.2 moles per liter of sulfuric acid. You task is to titrate a sample acid from a shipment of batteries to see if the concentration is within 5% of expected molar concentration. If 35.55 mL of 1.245 M NaOH solution is needed to neutralize 10.00mL of an H2SO4 solution, what is the molarity of the H2SO4 solution?
Above we discussed the strategy to solving this problem. When given "molarity" (M), change that to "moles per liter" (See columns C & D). You can see that when volume and concentration is multiplied, the "liter" units cancel giving you millimoles (mmoles). In column H when dividing by volume of H2SO4, the "milli" gets canceled.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
| 1 | mL of NaOH |
mL times molarity (moles/L) gives millimoles |
mole ratio 2:1 from balanced equation to get moles H2SO4 |
Divide by volume of H2SO4 to get moles per liter (M) |
molarity of H2SO4 |
||||||
| 2 | 65.05 |
mL |
1.245 |
moles NaOH | 1 |
mole H2SO4 | = |
4.048 |
moles | ||
| 3 | 1 |
Liter | 2 |
moles NaOH | 10.00 |
mL | Liter | ||||
The concentration is a little low but within the +/- 5% of the expected 4.2 M. The answer has 4 sig figs because all measurements are 4 sig figs. Your answer to #4 above should also have 4 sig figs because those measurements also have 4 sig figs. Note that the 2:1 ratio from the balanced equation are considered exact. Those are not measurements.
5. (a) How many moles of NaOH are contained in 50.0 mL of 0.125 M NaOH solution?
This problem is just like the first 4 columns of the practice problem above. However, you will have to get rid of the "m" in "mL" to get moles rather than millimoles.
A |
B |
C |
D |
E |
F |
G |
H |
|
| 1 | mL of NaOH |
mL times molarity (moles/L) gives millimoles |
cancel milli |
moles NaOH |
||||
| 2 | 50.0 |
mL |
0.125 |
moles NaOH | 0.001 |
= |
??? |
moles |
| 3 | 1 |
Liter | m |
|||||
5. (b) How many milliliters of 0.100 M H2SO4 solution would be needed to neutralize the above 50.0 mL of NaOH solution?
__NaOH (aq) + __H2SO4 (aq) --> __Na2SO4 (aq) + __H2O (l)
This equation was balanced in Problem 4. In this problem they are giving you the concentration of sulfuric acid (0.100 moles per liter) but asking for milliliters. That means the concentration of 0.100 M (moles per liter) will have to be inverted to get liters in the answer (in the numerator). The below setup shows the solving of 5b but also includes 5a in columns A-D. All units in red cancel. In dimensional analysis, placing the units in the numerator or denominator is decided by what units need to cancel and which need to remain.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
| 1 | mL of NaOH |
mL times molarity (moles/L) gives millimoles |
mole ratio 2:1 from balanced equation to get moles H2SO4 |
Concentration of H2SO4 is inverted so moles cancel and Liters will be in answer |
mL of H2SO4 |
||||||
| 2 | 50.0 |
mL |
0.125 |
moles NaOH | 1 |
mole H2SO4 | 1 |
Liter | = |
??? |
mL |
| 3 | 1 |
Liter | 2 |
moles NaOH | 0.100 |
moles H2SO4 | |||||
5 (c) How many grams of H2C2O4•2H2O (oxalic acid dihydrate) would be needed to neutralize 50.00 mL of the above NaOH solution (0.125 M)?
__NaOH (aq) + __ H2C2O4•2H2O (s) --> __Na2C2O4 (s) + __H2O (l)
Like before, the strategy is to find the moles of NaOH present, then convert that to moles of oxalic acid dihydrate using a balanced equation. Once you have moles, it's easy to change that to grams using the molar mass of oxalic acid dihydrate. To balance the above equation, use the trick of writing H2O as HOH. Also, keep track of the H2O in dihydrate separately. Below is a picture of oxalic acid. The two small white spheres are the acidic hydrogen atoms which come off to neutralize the OH in NaOH. Even without balancing the equation, we can see that it will take two NaOH molecules to balance the 2 hydrogen atoms coming from the oxalic acid dihydrate molecule. Balancing the above equation is just like the one in problem #3 except you need two NaOH molecules to balance with just one oxalic acid dihydrate molecule.
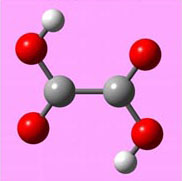The spreadsheet below shows the solving of 5a with the added steps to convert those moles into grams of oxalic acid dihydrate. Since we don't want the answer in milligrams, we need to cancel out the "m" from the "mL" in cell B2. "m" and "0.001" are equivalent.
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
|
| 1 | mL of NaOH |
mL times molarity (moles/L) gives millimoles |
mole ratio 2:1 from balanced equation to get moles H2SO4 |
Cancel "m" from mL |
Concentration of H2SO4 is inverted so moles cancel and Liters will be in answer | g H2C2O4•2H2O |
||||||
| 2 | 50.0 |
mL |
0.125 |
moles NaOH | 1 |
mole H2C2O4•2H2O | 0.001 |
126.066 |
grams | = |
??? |
g |
| 3 | 1 |
Liter | 2 |
moles NaOH | m |
1 |
moles H2C2O4•2H2O | |||||
In a spreadsheet, the formula in J2 would be "=A2*C2*E2*G2*H2/E2". What is nice about a spreadsheet is that you can change any one of the values and the new answer gets recalculated immediately.