1. Determine the density of a solid or liquid
2. Make a graph with experimental data.
3. Calculate the density using factor-label method.
4. Use correct number of significant figures.
Discussion: Density is a very useful property. It helps us identify unknown solids, liquids, or gases (See my diamond density example on lab 1 help page). It lets us know what will sink or float. Also, by knowing the density of something, we can figure out its weight if given the volume, or we can figure the volume if given how much it weighs.
Density is also useful because its a fairly easy property to measure. It only requires finding the weight of an object and its volume. Read about density in my measurement tutorial (density is about half way through the tutorial). Here's the link: http://www.chemistryland.com/CHM130W/02-MMM/Measure/Measuring.htm
Page 23.
A. Density of Water
Weigh a dry, clean 10 mL graduated cylinder. Remove the cylinder from the balance pan and add water to the 10mL mark (use medicine dropper to adjust). Weigh the cylinder and record the data. Calculate the density of water.
Page 24.
A. Density of Water
| Mass of cylinder + 10.00 mL of water | __________ g |
| Mass of empty cylinder | __________ g |
| Mass of water | __________ g |
| Volume of water | __________ g |
| Density of water | __________ g |
Calculation:
Your calculations will differ, but here is a sample calculation. Density is mass for one cubic centimeter (or one milliliter). Let's say the mass of 10.00 milliliters of water weighs 9.878 grams. To find density we only need the mass of 1 mL of water. That's easy; it is 9.8784 grams divided by 10. That gives us 0.98784 grams for one milliliter.
The calculation is written as follows:
9.8784 grams ÷10 = 0.98784 grams
10.00 mL ÷10 1 mL
This says 0.98784 grams per mL, which is a density measurement. The volume was only measured with 4 significant figures of accuracy and the mass was measured with 5 significant figures of accuracy. The final answer is only as good as the least accurate measurement. So we need to round the answer to only 4 significant figures. So the answer would be 0.9878 g/mL.
Page23.
B. Density of an Unknown Liquid
Sign out an unknown liquid from the stockroom. Record the number on your data sheet. Weigh a dry, clean 10 mL graduated cylinder. Remove the cylinder from the balance, and put exactly 2.0 mL of the liquid in the cylinder (use a medicine dropper as before) and weigh (Never add liquid when the cylinder in on the balance pan). Put another 2.0 mL of the liquid in the cylinder (reading should now be 4.0 mL) and weigh. Repeat for total volumes of 6.0 mL, 8.0 mL, and 10.0 mL. Pour the liquid back in the original container and return it to the stockroom. Calculate the density and make a graph with mL liquid on the x-axis (horizontal) and grams liquid on the y-axis (vertical). Draw the best straight line through the points (use a ruler). See the Appendix for graphing information.
(Note: The liquid is unknown to you but not to your instructor. The instructor knows what the density should be. If you were told what the liquid was, you could look up the density on the Internet without actually doing these measurements. But the whole idea is to do your own measurements and calculations. Also, this exercise is to show how you get essentially the same density answer whether you measure 2.0 mL or 10.0 mL. The 10.0 mL is more accurate because it has 3 significant figures of accuracy. )
The below graph shows how I set the spacing for the measurements. The data points were just made up but are close to what water should be. Water's density at 4 degrees Celsius is 1.0 g/mL. At room temperature, it is a little less.
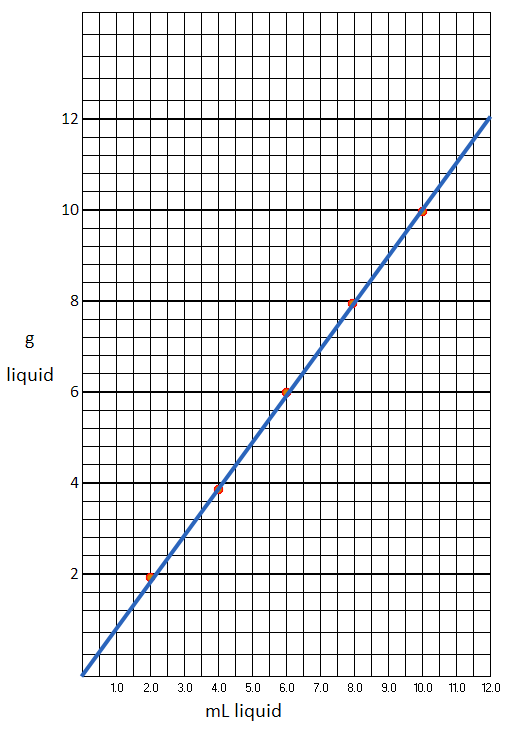
Page 27
Problems
Show your method clearly; include correct units in answers. Note that density can be used as a conversion factor. If the density of a liquid is 1.23g/mL, then the conversion factors are 1.23g/mL or 1mL/1.23g
1. From your graph on the previous page, find the mass of 5.8 mL of your unknown.
Using the graph, you would estimate where 5.8 mL is on the horizontal axis. You would go up from there and see where it hits the line. Then move to the left to read the grams. I'm estimating 5.8 grams. More accurate than the graph would be to use the average density that was calculated from all the measurements. If the average density was, let's say, 0.996 g/mL. You could multiply that times the 5.8 mL. Rounding to 2 significant figures comes out the same.
0.996 g x 5.8 mL = 5.7768 g > 5.8 g
1 mL
2. Based on your graph, how does the volume change with a decrease in the mass of the liquid.
Looking at our graph above, we can say, "As the mass (grams) decreases, the volume also decreases."
3. What is the density of a metal if 427.5 g of the metal occupies a volume of 35.0 mL?
Density is grams in one mL. So this is a simple division problem or actually, it is simply reducing the following fraction (note: grams is on top because density is g/mL):
427 g ÷ 35.0 = ?? g
35.0 mL ÷ 35.0 1 mL
This is a pretty dense metal. It's even more dense than lead, which is 11.3 g/mL.
4. Which measurement, the mass or the volume, would most likely be less accurate, giving error in the calculated density? Explain.
The volume is often the less accurate measurement. A graduated cylinder can only be measured with 3 or 4 significant figures (examples 10.3mL or 35.15mL). An analytical balance can have 4, 5, 6, and even 7 significant figures depending on the mass and the balance (examples: 0.9876 g or 123.6543 g.)
5. A solid cube, 2.20 cm on an edge weighed 6.488 grams. Will it sink or float in water? Explain.
First we find the volume of a cube: 2.20 cm x 2.20 cm x 2.20 cm = 10.658 cm3.
6.488 g ÷ 10.658 = ??? g
10.658cm3 ÷ 10.658 1 cm3
Notice we round the answer to 3 significant figures because "2.20 cm" had 3 sig figs.
6. An oil has a density of 1.44 g/mL. How many mL is needed for 22.036 grams?
First of all, this oil is more dense than water (>1.00g/mL). Most oils are lighter, which is why most oils float on water. Most oils are made with only carbon and hydrogen. That makes them light. This oil must have some heavier elements like chlorine, bromine, or iodine. These can replace some of the hydrogen atoms.
Using the factor-label method we see that our answer has to be in mL, and we are starting with grams.
22.036 grams >>>>> ? mL
To get rid of grams and have mL, we can use the density of 1.44g/mL but we have to invert it.
22.036 g x 1 mL = ??? mL (round to 3 sig figs)
1.44g
7. In an experiment to determine the density of an unknown liquid, the sample was spilled. Write out the steps for a procedure to determine the density of a liquid if less than 6.0 mL of the sample is available.
A 10 mL graduated cylinder would give you about 2 significant figures of accuracy. Its markings are 0.1 mL, but you can estimate between markings to get perhaps another significant figure. Something more accurate is a volumetric pipette. See image on the right. A 5mL volumetric pipette is accurate to a 0.01 mL, so that guarantees 3 significant figures. They also make 4, 3, 2, and 1 mL versions if there's less than 5mL.
First you would weigh a small beaker (25 mL). You would then draw the liquid into the 5mL volumetric pipette until you got the meniscus to the fill mark (blue arrow in picture). Then release the liquid into the weighed 25 mL beaker. Now weigh the beaker again. Subtract the mass of the beaker to find the mass of the 5mL of liquid. Divide that liquid's mass by 5mL to get density. Give density with 3 significant figures.
