Balancing Chemical Equations
Chemical Equations vs. Math Equations
60 =
20 + 8x

H2CO3
-> H2O + CO2
Reactants ->
Products
When you see the name "chemical equations,"
the word "equation" makes us think of math equations. There
is some similarity. Like all equations, something has to be "equal."
In a math equation the value of the left side of the equal sign is the
same value as the right side. These values also exist at the same time
like a balance.
In a chemical equation the atoms on the left side have to be equal to
the atoms on the right side of the arrow, but they don't exist at the
same time. The chemical equation represents movement. For example, here
we start with carbonic acid consisting of 2 hydrogen atoms, 1 carbon atom,
and 3 oxygen atoms. The atoms rearrange and become water and carbon dioxide.
All original atoms are still accounted for.
Chemical Equations are simple:
Like I said earlier, atoms combine in simple ratios. That
means the chemical equations that show and balance the starting "reactants"
and ending "products" are fairly simple. Unlike math equations,
chemical equations are showing a progression of time.
Here we see how hydrogen and oxygen (reactants) react and produce water.
It's a simple rearrangement.
Roll mouse over image to see animation.

Bike Example for Balancing Chemical Equations:
We are all familiar with bicycles, tricycles, etc. It's also easy to see how many wheels are necessary to build them. Because this is very visual (and atoms are too small) I'm going to use the manufacturing of these products as an introduction to balancing chemical equations.

This company is going to promote their super durable tires. The tires will be the biggest expense in making these cycles. Because of that, the company may recall cycles that aren't celling and put the wheels on the cycles that are selling.
Notice that the wheels are only sold to the manufacturer in pairs.

The company that produces these pedal cars can use abbreviations similar to the way chemistry uses abbreviations. For example Cb can represent the "Car body". "W" will represent the "wheels." Remember that the wheels are only purchased in pairs. So "W2" repesents a pair of wheels. The production scheme is that one car body (Cb) is added to two pairs of wheels (2W2) to make a complete car (CbW4).
We know a car has four wheels, so the formula of CbW4 should seem logical.
The approach in balancing chemistry equations uses the same logic.
We
need fire extinguisher fluid (carbon tetrachloride)
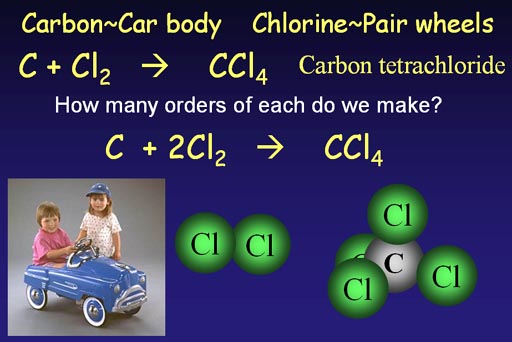

The carbon "C" is like the car body. Chlorine always comes as a pair, so it's like the wheels that come in pairs.
To make carbon tetrachloride we need carbon and chlorine.
C + Cl2 -> CCl4
This is the unbalanced chemical equation because the number of chlorine
atoms in the product is different than what we started with. We are 2
chlorine atoms short, so we show two pairs of chlorines.
C + 2Cl2 -> CCl4
This is the balanced chemical equation.

When we manufacture tricycles, we run into a problem. We know we need to add wheels (W2) to a trike body (Tb). This gives us the unbalanced equation:
Tb + W2 -> TbW2
As you can see this number of wheels don't match. If we use two pairs of wheels (2W2), we end up with an extra wheel. So we compensate by starting with two trike bodies. Then we are short wheels, so we go with 3 pairs. At this point we the number of trike bodies and wheels we start with match what we end with; so it's now a balanced production equation.
Making aluminum chloride
(anti-perspirant ingredient)
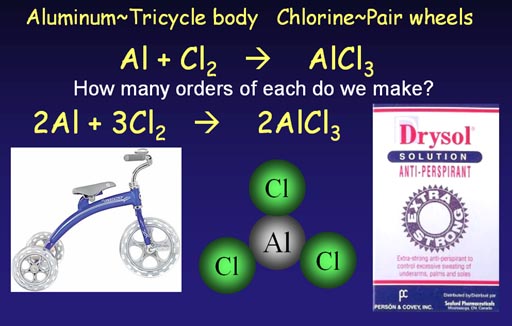
(anti-perspirant ingredient)

A trike body attaches to 3 wheels. Aluminum attaches to
3 chlorine atoms. Because of this similarity, the equation for making
aluminum chloride has the same issues. We start with an unbalanced (skeleton)
chemical equation.
Al + Cl2 -> AlCl3 (short 1 chlorine at start)
Al + 2Cl2 -> AlCl3 (ends up with extra
chlorine)
2Al + 2Cl2 -> 2AlCl3
(short 2 chlorines at start)
2Al + 3Cl2 -> 2AlCl3 (all atoms match)
We see that starting with Cl2 is not enough chlorine atoms, so we go with 2Cl2 but then end up with an extra chlorine atom. So we go with 2 aluminum atoms, but then we are short 2 chlorine atoms. Finally, by going with 3 pairs of chorines atoms, we end up with a balanced equation.
Cars not selling, so use car wheels to make bicycles

So far we've done a simple synthesis where one thing is
built from simpler pieces. Now we will do what's called a "single
replacement" or "single displacement" reaction. That's
when one part is replaced (displaced) with another. In this example, the
car body is being replaced with a bike body. The wheels are being reused.
In our unbalanced (skeleton) equation, we simply write that we start with
a bike body and car with wheels and end up with a full bike and car body
without wheels. Unfortunately the number of wheels don't match. A manufacturer
would go bankrupt if it doens't know how to get the proper number of starting
materials so that there's no leftover pieces at the end of the production.

Looking at the unbalanced equation, we see that the number of wheels on the left side (4 wheels) are twice as many as those on the finished side (2 wheels). So we see that if we finished with 2 bicycles, we would use all 4 wheels. To finish with two bicycles we have to start with 2 bicycle bodies. Now we have a balanced equation.
Anti-perspirants not selling, we need
de-icers. Let's use the chlorines from one to make the other.

A chemistry example equivalent to the above example is changing carbon tetrachloride (fire extinguisher fluid) to calcium chloride (deicer powder).
Like the above example, the carbon tetrachloride has twice the chlorine atoms than the calcium chloride needs. This forces us to double the final calcium chloride compounds, which also means we must start with two calcium atoms. This is called a single replacement reaction because the carbon in carbon tetrachloride molecule gets replaced with a calcium atom.

3Ca + 2AlCl3 -> 2Al + 3CaCl2
Here is another tricky one. We are taking tires off of trikes to make wagons. As you can see trikes has 3 wheels and wagons have 4 wheels. Let's see if you can do it. My only hint is 4x3=3x4.
Roll mouse over image to check your answer.
So far the wheels are simply transferred a different body. Now let's try some double swapping.

Let's say we have Three-wheeled fuselage [Tf] connected
to a rotor [R] (top image) and we want to take the wing off of a car fuselage
[CfWi] (bottom image) and make a winged 3-wheel fuselage [TfWi] (middle).
The car would then get the rotor (not shown): Here's the equation.
TfR
+ CfWi -> CfR
+ TfWi
Looking at this equation we see that the fuselages simply swapped places. The three-wheel fuselage that had a rotor now has a wing and the car fuselage that had a wing now has a rotor.
They call this a "double-replacement" or "double-displacement" reaction (no big surprise).
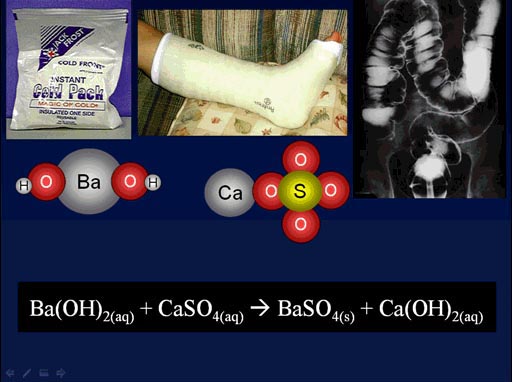
Here is a chemistry example that was shown in an earlier tutorial. This is also a double-replacement reaction.
Here the barium atom swaps places with the calcium atom. When that happens, we make barium sulfate which is given to patients to drink, so x-rays can see the stomach and intestines. As a kid I had to drink it, and it tasted like chalk. It was bad. They could have at least sweetened it.
(roll cursor over image to see the double-replacement animation)

The point I want to make with this tutorial is that the techniques of balancing the starting and ending amounts are useful to chemistry or any kind of production.
In a later tutorial, we will expand this analogy and deal with handling large quantities of starting items (reactants) and products.


