Most textbooks teach significant figures with a set of rules. I don't like that approach because rules don't teach you why. You are just following the rules blindly. Not much learning happens there. Let's take a closer look at how you get significant numbers. |
| The below image is that of a shoeprint at a crime scene. A ruler is superimposed to do a measurement between a corner of one pattern to the edge of another pattern. This measurement could be used to find the shoe that made the impression, which finds the person who left his or her shoeprint at the crime scene. Let's say the examiner wrote down the distance as 10 centimeters. Unfortunately, 10 cm is ambiguous. Was it 11 cm that got rounded down to 10 cm or was it 8 cm that got rounded up to 10cm? If the examiner wrote "10.", the decimal point means he or she measured it to the nearest centimeter. In other words, the measurement was less than 10.5 centimeters, but greater than 9.5 centimeters. If the examiner wrote 10.3 centimeters, it means it was measured to the nearest tenth of a centimeter. The figures in "10.3" are all significant. The "1" means there were about 10 centimeters of length. The "0" means there were no whole centimeters to add, and the ".3" means there were 3 tenths of a centimeter extra length. That's 3 significant figures. With a good eye an examiner can look between the two millimeters lines (tenths of a centimeter) and estimate that the edge was about half way in between those lines. That means he or she could write down the distance as "10.35" centimeters, which has 4 significant figures. It was very important to have enough accuracy (enough significant figures) to allow police officers to see if they had a shoe that matched this print. |
|
|
This is a digital balance like the one students use in my portable lab kit for CHM107. It measures to the nearest tenth of a gram. Let's say I had them weigh out some baking soda and it weighed 40.3 grams. That is 3 significant figures because each figure is contributing to the measurement. In other words, the "4" says there are 40 grams. The "0" says there where no single grams. And the ".3" says there were 3 tenths of a gram extra. They all contribute to the final weight of 40.3 grams. They all are significant figures. Even the zero in between 4 and 3 is giving us information. Now let's say we need to use this weight in a formula that needs the weight in kilograms. Turning 40.3 grams into kilograms gives us 0.0403 kilograms. Now we have two zeros in front of the 403. Does that mean the weight now has 5 significant figures? No, the measurement can't get more accurate by simply changing the units. Those zeros to the left of the 403 are not significant. They are only there to place the decimal point correctly when going from grams to kilograms. So these leading zeros are not counted as being significant. |
|
The above example showed how converting from grams to kilograms (40.3 g > 0.0403 kg) implied a change of accuracy, but you learned that the leading zeros are not counted. The same thing can happen going the other way. If we converted 40.3 grams to milligrams, the measurement becomes 40,300 milligrams. That looks like 5 significant numbers but, again, we can't get more accuracy by simply changing the unit of measurement. So those zeros after the 403 don't count. In that way we retain the same 3 significant figures. |
|
Let's do another example with a weight measurement. In a lab I say you need 50 grams of sugar to do the experiment. By saying "50 grams" I am implying that the sample can be between 45 and 55 grams. "50" has only one significant figure (5), which means its accurate only to the nearest 10 grams. Not realizing that, a student worked hard to get the sample to show 50.0 grams on the readout. That's 3 significant figures because it was measured to have 50 grams with zero single grams and zero tenths. So the zeros in "50.0" are giving real information about the weight. If the students simply reported they weighed out 50 grams, I could only assume it was rounded. By reporting "50.0 grams" I will assume they took the effort to measure it down to a tenth of a gram. Note: If a situation asked for 50.00 grams of sugar, this balance could not measure to that accuracy. So the point is 50 g, 50.0 g, and 50.00 g are not the same weights. In math, 50, 50.0, and 50.00 are all the same number. But when they are measurements, they are not. |
|
Using money is a good lesson in significant figures. Let's say you and a friend were going to buy tickets to a concert. The tickets are $30. You call a friend and ask how much money does he have on him. He glances in his wallet and tells you he has $30. You have $30.25 so you know you're good. When you meet him at the ticket window, you find out that he actually has only $29 and 35 cents. So you don't have the $60 to get the two tickets. When you heard your friend say $30, you can only assume that he rounded the money to the nearest $10. He may have had $26 or $34. $30 has only one significant figure. If he said $29, then you know he's rounding the amount to the nearest dollar. So he's between $28.50 and $29.50. However, if he told you he had $29 and 35 cents, he's giving you 4 significant figures. Also, if you told him you have $30 and 25 cents. He knows the $30 is not rounded because you are including the 25 cents. So $30.25 also has 4 significant figures. That zero that sits between 3 and 2 is an accurate measurement saying there are no single dollars. |
|
Significant number is calculations:
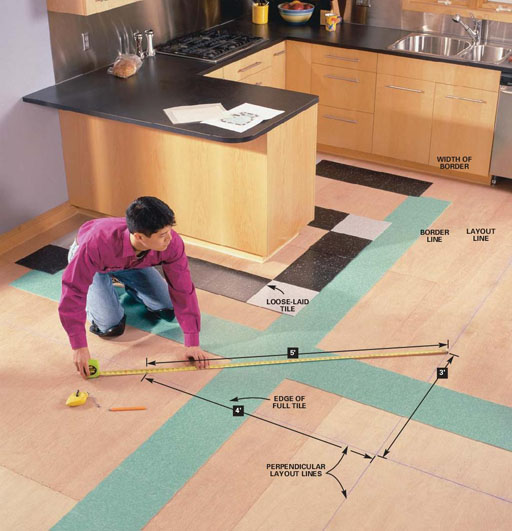
Laying tile involves accuracy, so significant figures are useful. Let's say you want to know how wide 10 tiles would go. You measure one tile and you get 11 7/8 inches on one side of the tape measure and 30.2 centimeters on the other side. If you convert 11 7/8 inches to decimal fraction, you get 11.875 inches. That implies accuracy down to a thousands of an inch. That isn't true because the tape can't measure to the nearest thousandths of an inch. Only to the nearest 16th of an inch. So significant numbers are easier to determine when a measurement is done with decimal fractions. So the width of 10 tiles at 30.2 centimeters per tile would be 10 x 30.2 cm = 302 cm. You might wonder how many significant figures are in 10 tiles. Because the tiles are counted, the accuracy is exact. So we don't have to worry about the significant figures in the 10 of 10 tiles. To find the area of a 10 tile by 10 tile square, we would multiply the width 302 cm by the length, which is also 302 cm (tiles are square). We get an area of 302x302=91204 square centimeters (cm2). "91204" has 5 significant figures and implies that we know the area down to a single square centimeter. That's not true. The accuracy of our measurement was only to 3 significant figures. So when multiplying or dividing, our answer can only be trusted to be accurate to 3 significant figures. So 91204 cm2 needs to be rounded to 91,200 square centimeters. This means we can only guarantee accuracy of the area to the nearest 100 square centimeters. |
 |
Speaking of area, let's say you need carpet and you need the square feet. You measure the length to be 12.5 feet and your helper measured the width to be 11 feet. In other words, your helper only measured to the nearest foot. So your measurement had 3 significant figures because you measured to the nearest tenth of a foot. Your helper's measurement was only 2 significant figures. (note: I will call significant figures "sig figs" for short). To find area of the room, you multiply width times length. So that's 11ft x 12.5 ft =137.5 square feet. "137.5 sq. ft." implies that you know the area to the nearest tenth of a square foot. Also, "137.5 sq. ft." has 4 sig figs. The accuracy of your answer is only as good as the least accurate measurement. That's because the "11 ft" is between 10.5ft and 11.5 ft, meaning your multiplication could have been 10.5 ft x 12.5 ft = 131.25 sq. ft or 11.5 ft x 12.5 ft = 143.75 sq. ft. So you see there's a spread of about 12 sq. ft. difference between the two. So you can't just multiply 11ft x 12.5 ft and expect the 137.5 sq. ft. is accurate. So the way to give an answer that reflects the true accuracy, is to realize that "11 ft" only has 2 sig figs, so we round off the 137.5 sq. ft. to also have only 2 sig figs. That becomes 140 sq. ft. Someone seeing "140 sq. ft." would realize that means the accuracy is only to the nearest 10 sq. ft., which is a true reflection of what we know from these measurements. In other words, the area is between 135 sq. ft. and 145 sq. ft. |
 |
Just out of high school I worked for a construction company that had a fuel storage tank that needed to be filled. The supervisor asked me to go get the measurements. I measured the height as 4.457 meters (that's to the nearest millimeter). It was hard to measure the diameter, so I called it 2 meters. Volume of a cylinder is V=height x pi x r2. If diameter is 2 meters the radius is 1 meter. So the calculation was 4.457 meters x pi x (1 meter)2. For pi I used 3.14. So the answer came out to be 13.99498 cubic meters. As you might guess, this shows an accuracy much more than can be justified. Even though the 4.457 meter measurement had 4 sig figs, the measurement of 2 meters was only 1 sig fig, so the answer would have to rounded to 1 sig fig. Therefore, "13.99498" is rounded to 10 cubic meters. That wasn't good enough for the supervisor. So I went out to measure the diameter again. This time I measured the circumference, which was easy to do. I got 6.753 meters as the circumference. The formula for circumference is C=pi x D. So to solve for diameter, I divided my circumference by pi. You can look up pi to any number of sig figs. Since my measurement of 6.753 meters had 4 sig figs, I used a value of pi that had at least 4 sig figs otherwise, it would cause the answer to be less accurate. So I used 3.1416 with 5 sig figs. So 6.753 meters divided by 3.1416 gave me a diameter of 2.14954 meters, which is a radius of 1.07477 meters. Using the volume formula again, I got V=(height) 4.457 meters x pi (3.1416) x radius2 (1.07477 meters)2. V=16.17427 cubic meters. That should be rounded to 4 sig figs; however, I first want to convert that to gallons. So I look up the conversion of cubic meters to gallons and find 1 cubic meter = 264 gallons, but then found another source that had 1 cubic meter = 264.172052 gallons. The first only was accurate to 3 sig figs, but I wanted 4 sig figs or better, so I used 1 cubic meter = 264.17 gallons. So multiplying 16.17427 cubic meters times the 264.17 gallons per cubic meter gave me 4,272.76 gallons. That has 6 sig figs, which isn't justified. Our two measurements are good to 4 sig figs, so we can round our answer to 4 sig figs. So 4,272.76 gallons becomes 4,273 gallons, which we are confident is accurate to the nearest gallon. A fuel truck was ordered to bring 4,270 gallons, and we were confident it would fill the tank up without spilling over. Of course, then depends on them having the same degree of accuracy with their measurements. |
1. Zeros between numbers are actual measurements and are significant. (103, 0.0403, 2001, 0.002001, etc.)
2. Zeros to the right of whole numbers where there is no decimal point are NOT significant because those can result from unit conversion. (300, 20, 4000, etc.)
3. Zeros to the left of decimal fractions are NOT significant also because they can be from unit conversion (0.03, 0.0045, 0.678, 0.000201, etc.)
4. Any zero in a number written in scientific notation is significant except for the zero in the "x 10" (3.0x102, 4.100x103, 6.0780x104, 7.000x1020, etc.) |
To summarize, we see that zeros between figures are significant. For example, 3004 has 4 sig figs because all figures including the zeros were actually measured. But 3000 has only one sig fig because the zeros could be there simply from a conversion of one unit to another. In 0.00450 the zeros on the left are not significant because they could be there from a conversion to another unit; however, the zero on the right is indicating that a measurement was taken to one more level below the "5". So 0.00450 has 3 significant figures. |